我的博客

题解

这里有篇很好的文章，对于深入理解有帮助

对于这道题目，第一想法就是用bool数组标记，最后统和，但是奈何数据范围不允许。

可以用扫描线+线段树维护，但是总觉得有点大动干戈。

而“离散化”这一奇妙的思想能帮我们优雅地解决这道题（然而样例不能很好体现）

我们首先来看看样例



其中一样的颜色的点为一对输入（一个矩形），我们取出它们的横纵坐标，去重，排序，然后再去枚举，就得到了那些黑色的点。（有些和有颜色的点重复了）

其实到了这一步我们已经离散化了（还没明白?别急，先往下看）

于是我们枚举每一个黑色的点，让它和它右上方的黑点构成一个矩形，如果这个矩形在任意输入矩形内部，则对答案有贡献

这样子我们就做到了不重不漏(黑点枚举出来的矩形不重复，并且黑点构成的全部矩形肯定把输入矩形囊括在内)

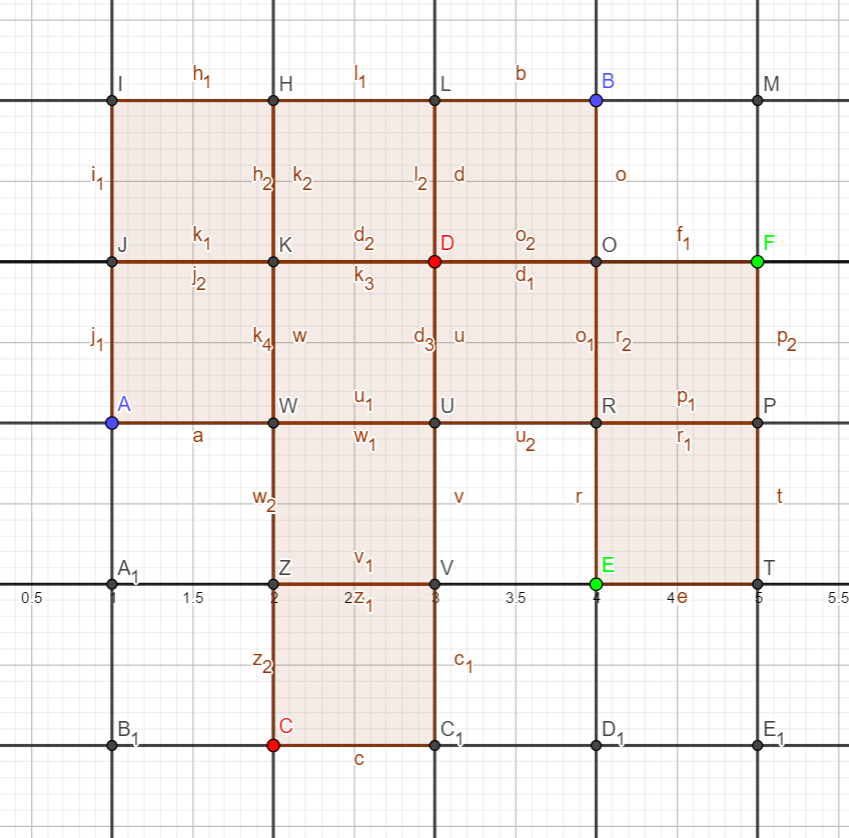
到这里貌似就结束了，但是这种方法看上去还是在数格子？

让我们把输入改成


3
1 1 4 4
2 -1 3 3
4 0 5 3

再看看图像


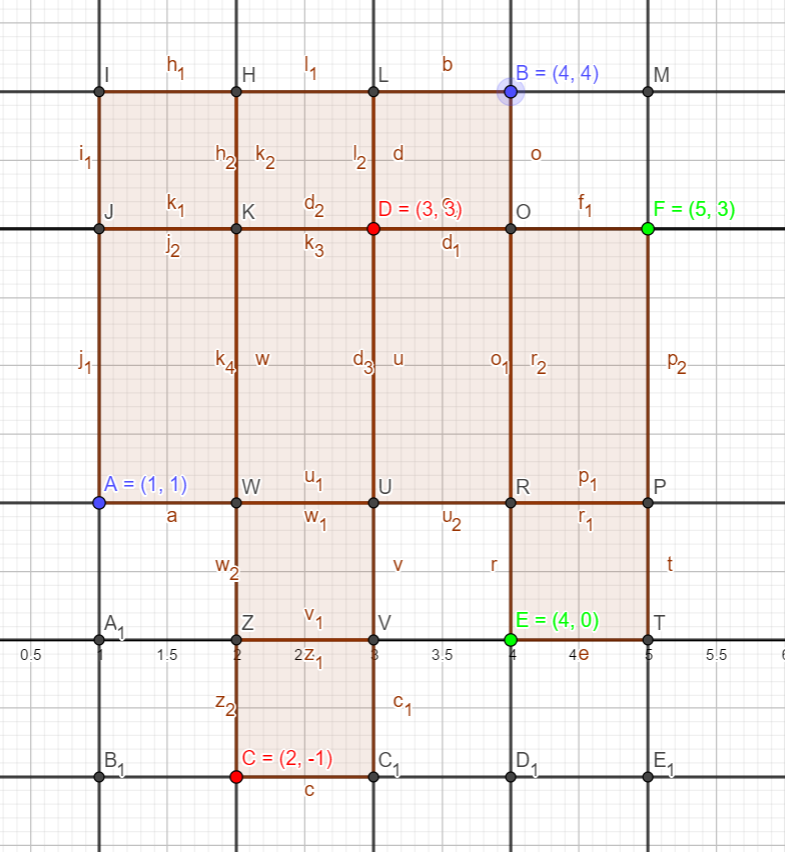
我们的枚举量并没有随着坐标范围变大而变大，并且还是做到了不重不漏，其原因就是我们在枚举黑点的时候，本来是2的距离，转化成了该点与上个点相差2，而空间上这两个点还是相邻的，这就是离散化。

上面已经解释得很清楚了，代码就不写注释了。

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN=203;
long long x[MAXN],y[MAXN],x1[MAXN],x2[MAXN],y1[MAXN],y2[MAXN];
long long S,ans;
int n;

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%lld%lld%lld%lld",&x1[i],&y1[i],&x2[i],&y2[i]);
        x[2*i-1]=x1[i];
        y[2*i-1]=y1[i];
        x[2*i]=x2[i];
        y[2*i]=y2[i];
    }
    sort(x+1,x+2*n+1);
    sort(y+1,y+2*n+1);//这里忘了去重，如果有重复的，(x[i+1]-x[i])*(y[j+1]-y[j])必定有一项为0，对答案没贡献
    for(int i=1;i<=2*n-1;i++){
        for(int j=1;j<=2*n-1;j++){
            S=(x[i+1]-x[i])*(y[j+1]-y[j]);
            for(int k=1;k<=n;k++){
                if(x[i]>=x1[k]&&y[j]>=y1[k]&&x[i+1]<=x2[k]&&y[j+1]<=y2[k]){
                    ans+=S;
                    break;
                }
            }
        }
    }
    cout<<ans;
    return 0;
} 

题目都说了是矩形。。。输入还能不合法。。。出题人心里没点高数吗

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define N 1001
using namespace std;

long long n,num=1,Num=1,lfx[N],lfy[N],rtx[N],rty[N],x[N],y[N],a[N],b[N];
long long flag[N][N],rec[N][N],ans;

int main()
{
    scanf("%d",&n);
    
    for(int i=1;i<=n;i++){
        cin>>lfx[i]>>lfy[i]>>rtx[i]>>rty[i];
        a[2*i-1]=lfx[i];a[2*i]=rtx[i];
        b[2*i-1]=lfy[i];b[2*i]=rty[i];
    }
    sort(a+1,a+1+2*n);
    sort(b+1,b+1+2*n);
    x[1]=a[1],y[1]=b[1];
    for(int i=2;i<=2*n;i++){
        if(a[i]!=a[i-1])
            x[++num]=a[i];
    }
    for(int i=2;i<=2*n;i++){
        if(b[i]!=b[i-1])
            y[++Num]=b[i];
    }
    for(int i=1;i<=num-1;i++)
        for(int j=1;j<=Num-1;j++)
            for(int k=1;k<=n;k++)
                if(x[i]>=lfx[k]&&x[i+1]<=rtx[k]&&y[j]>=lfy[k]&&y[j+1]<=rty[k])
                    flag[i][j]=1;
    for(int i=1;i<=num-1;i++)
        for(int j=1;j<=Num-1;j++)
            rec[i][j]=abs((x[i+1]-x[i])*(y[j+1]-y[j]));
    for(int i=1;i<=num-1;i++)
        for(int j=1;j<=Num-1;j++)
            if(flag[i][j])
                ans+=rec[i][j];
    cout<<ans;
    return 0;
}

排序离散化，卡在#4，晕死~~矩阵还可以是不合法的~~cheat了#4才AC~

神奇的离散化~膜拜Matrix67神牛~~

居然因为数据没开到int64交了N次。。。。

很水的一道题，我就不多说啦，就直接离散，关键操作我就注释代码里面啦。。。。。。
```cpp
#include<iostream>
#include<cstdio>
#define MAX 250
using namespace std;
long long n,x1[MAX],y1[MAX],x2[MAX],y2[MAX],ans;
long long zb[2][MAX*2];//嫌麻烦,直接把x和y存在一起了,zb[0]表示x,zb[1]表示y

void quicksort(long long left,long long right,long long k)
{
long long i,j,mid,t;
i=left; j=right; mid=zb[k][(i+j)/2];
while (i<j)
{
while (zb[k][i]<mid) i++;
while (zb[k][j]>mid) j--;
if (i<=j)
{
t=zb[k][i]; zb[k][i]=zb[k][j]; zb[k][j]=t;
i++; j--;
}
}
if (left<j) quicksort(left,j,k);
if (i<right) quicksort(i,right,k);
}

int main()
{
scanf("%I64d",&n);
for (int i=1; i<=n; i++)
{
scanf("%I64d %I64d %I64d %I64d",&x1[i],&y1[i],&x2[i],&y2[i]);
ans++;
zb[0][ans]=x1[i]; zb[1][ans]=y1[i];
ans++;
zb[0][ans]=x2[i]; zb[1][ans]=y2[i];
}

quicksort(1,2*n,0);
quicksort(1,2*n,1);

ans=0;
for (int i=1; i<2*n; i++)
for (int j=1; j<2*n; j++)
{
long long mj=(zb[0][i+1]-zb[0][i])*(zb[1][j+1]-zb[1][j]);
for (int k=1; k<=n; k++)//判断有没有原来的矩形覆盖当前枚举的i,j;
if (zb[0][i]>=x1[k]&&zb[0][i+1]<=x2[k]&&zb[1][j]>=y1[k]&&zb[1][j+1]<=y2[k])
{
ans+=mj; break;//找到就直接退出循环k
}
}

printf("%I64d",ans);
return 0;
}
```

题解与楼下某位的思路类似
不用离散化，暴力过
代码如下（由于非常好懂，就不多解释了）

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <vector>
#include <map>
#define N 1000000+100
using namespace std;
long long n,nx,ny,ans,sum1,sum2,leftx[501],lefty[501],rightx[501],righty[501],flag[501][501],rec[501][501],x[501],y[501];
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>leftx[i]>>lefty[i]>>rightx[i]>>righty[i];
        x[++sum1]=leftx[i];
        y[++sum2]=lefty[i];
        x[++sum1]=rightx[i];
        y[++sum2]=righty[i];
    }
    sort(x+1,x+1+sum1);
    sort(y+1,y+1+sum2);
    for(int i=1;i<=sum1;i++)
        if(x[i]!=x[i-1])
            x[++nx]=x[i];
    for(int i=1;i<=sum2;i++)
        if(y[i]!=y[i-1])
            y[++ny]=y[i];
    for(int i=1;i<=nx-1;i++)
        for(int j=1;j<=ny-1;j++)
            rec[i][j]=abs((x[i+1]-x[i])*(y[j+1]-y[j]));
    for(int i=1;i<=nx-1;i++)
        for(int j=1;j<=ny-1;j++)
            for(int k=1;k<=n;k++)
                if(x[i]>=leftx[k]&&x[i+1]<=rightx[k]&&y[j]>=lefty[k]&&y[j+1]<=righty[k])
                    flag[i][j]=1;
    for(int i=1;i<=nx-1;i++)
        for(int j=1;j<=ny-1;j++)
            if(flag[i][j]==1)
                ans+=rec[i][j];
    cout<<ans;
    return 0;
}

编译通过...├ 测试数据 01：答案正确...ms├ 测试数据 02：答案正确...ms├ 测试数据 03：答案正确...ms├ 测试数据 04：答案正确...ms├ 测试数据 05：答案正确...ms├ 测试数据 06：答案正确...ms├ 测试数据 07：答案正确...ms├ 测试数据 08：答案正确...ms├ 测试数据 09：答案正确...ms├ 测试数据 10：答案正确...msAccepted 有效得分：100 有效耗时：0ms

离散化+线段树。。。

按x离散化并建立线段树，然后把平行于x轴的扫描线插入到线段树中，算出实时覆盖长度，然后就不用我说了吧、、、、、

PS. 强烈BS楼下的 题解王： 赫敏·格兰杰

Accepted 有效得分：100 有效耗时：0ms

50分的同志们注意一下,答案是int64的 T^T

如果还是50分的同志们在注意一下,int64是不能要inc的 T^T

今天我彻底悲剧了 T^T

在 275616951 大牛的指导下

我成功地

AC!!!!!!!!!!

orz 275616951 大牛

program p1056;

type node=record

x1,x2,y1,y2:longint;

end;

var w:array[1..200]of node;

i,n:longint;

ans:int64;

procedure init;

var i,j:longint;

begin

readln(n);

for i:=1 to n do

readln(w[i].x1,w[i].y1,w[i].x2,w[i].y2);

end;

procedure cut(x1,x2,y1,y2:int64;t:longint);

begin

if (x1>=x2)or(y1>=y2) then exit;

while (t>=1)and((x1>=w[t].x2)or(x2=w[t].y2)or(y2

靠...int64....

为此我WA了，n次....

通过率这么低的原因是：

1：int64；（没有40分）

2：输入的矩形不一定合法（没pd90）

INT64

├ 测试数据 01：答案正确... 0ms

├ 测试数据 02：答案正确... 0ms

├ 测试数据 03：答案正确... 0ms

├ 测试数据 04：答案正确... 0ms

├ 测试数据 05：答案正确... 0ms

├ 测试数据 06：答案正确... 0ms

├ 测试数据 07：答案正确... 0ms

├ 测试数据 08：答案正确... 0ms

├ 测试数据 09：答案正确... 0ms

├ 测试数据 10：答案正确... 0ms

---|---|---|---|---|---|---|---|-

Accepted 有效得分：100 有效耗时：0ms

离散,更快更好写

编译通过...

├ 测试数据 01：答案正确... 0ms

├ 测试数据 02：答案正确... 0ms

├ 测试数据 03：答案正确... 0ms

├ 测试数据 04：答案正确... 0ms

├ 测试数据 05：答案正确... 0ms

├ 测试数据 06：答案正确... 0ms

├ 测试数据 07：答案正确... 0ms

├ 测试数据 08：答案正确... 0ms

├ 测试数据 09：答案正确... 0ms

├ 测试数据 10：答案正确... 0ms

---|---|---|---|---|---|---|---|-

Accepted 有效得分：100 有效耗时：0ms

矩形分割，既快又好写~

不是说“坐标范围为–10^8到10^8之间的整数。”吗？为什么用longint还是不行？分明是题目有问题嘛。

编译通过...

├ 测试数据 01：答案正确... 0ms

├ 测试数据 02：答案正确... 0ms

├ 测试数据 03：答案正确... 0ms

├ 测试数据 04：答案正确... 0ms

├ 测试数据 05：答案正确... 0ms

├ 测试数据 06：答案正确... 0ms

├ 测试数据 07：答案正确... 0ms

├ 测试数据 08：答案正确... 0ms

├ 测试数据 09：答案正确... 0ms

├ 测试数据 10：答案正确... 0ms

---|---|---|---|---|---|---|---|-

Accepted 有效得分：100 有效耗时：0ms

万恶的数据。。。万恶的int64，同样的程序，只是数据类型的差异，竟然害我WA了三次；

虽然如此。。。还是在此Orz 一下Matrix67神牛，真是神奇的离散化。。

这题讲两个做法：

一种是离散化，也就是将原平面，对于每一个Y坐标，做直线Y=Yi,对每个X坐标，做直线X=Xi，此时分成很多个矩形，则这些矩形要么被某个矩形完全覆盖，要么不被任何矩形覆盖（相交）。

则可以模拟一条扫描线，维护每两条相邻的竖线之间有多少个小矩形被覆盖即可。每一个小矩形可以用一个Y坐标来离散。

第二种做法是朴素，也就是扫描线过去，把相应位置染色，实现的时候，在添加区间时，若走到了个新区间则开一个新空间给这个位置并继续下传，询问的时候，如果儿子为空则表示对应区间没有被染色。这样就可以用nlogn的空间解决这道题了。

hint:线段树区间负数正数都有的时候，若当前区间为(l,l+1)，那一定要记得讨论分区间，不然会死循环

很神奇的离散❀撒