#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#include <vector>
#include <deque>
#include <set>
#include <limits>
#include <string>
#include <sstream>
using namespace std;

namespace dts
{
    typedef long long ll;
    
    //splay
    ll size;
    ll fa[3000000+1];
    ll s[3000000+1][1+1];
    ll sl[3000000+1];
    ll sr[3000000+1];
    ll len[3000000+1];
    //splay
    
    struct splay
    {
        ll root;
        
        ll insert(ll l,ll r)
        {
            size++;
            fa[size]=s[size][0]=s[size][1]=0;
            len[size]=(sr[size]=r)-(sl[size]=l);
            //interval  [l,r) [l,r-1]
            return size;
        }
        
        ll pr(ll l,ll r)
        {
            return (root=insert(l,r));
        }
        
        ll update(ll now)
        {
            return (len[now]=len[s[now][0]]+len[s[now][1]]+sr[now]-sl[now]);
        }
        
        ll dir(ll now)
        {
            //left or right
            return ((s[fa[now]][1]==now)?1:0);
        }
        
        void rotate(ll now)
        {
            ll nowdir=dir(now),nowfa=fa[now];
            fa[now]=fa[nowfa];
            if (nowfa==root)
                root=now;
            else
                s[fa[nowfa]][dir(nowfa)]=now;
            if ((s[nowfa][nowdir]=s[now][nowdir^1])!=0)
                fa[s[nowfa][nowdir]]=nowfa;
            fa[s[now][nowdir^1]=nowfa]=now;
            update(nowfa);
            update(now);
        }
        
        void splay_work(ll now)
        {
            for (;fa[now];rotate(now))
                if (fa[fa[now]]!=0)
                    rotate((dir(now)==dir(fa[now]))?fa[now]:now);
        }
        
        ll split(ll now,ll x)
        {
            x+=sl[now];
            //pre x number not change
            //behind number move to new node
            ll ans=insert(x,sr[now]);
            //ans   new node
            sr[now]=x;
            if (s[now][1]==0)
                fa[s[now][1]=ans]=now;
            else
            {
                ll t;
                //t temp
                for (t=s[now][1];s[t][0]!=0;t=s[t][0])
                    ;
                fa[s[t][0]=ans]=t;
                for (;t!=now;t=fa[t])
                    update(t);
            }
            splay_work(ans);
            return ans;
        }
        
        ll pop(ll x)
        {
            //pop x th number
            ll now,flag;
            for (now=root,flag=1;flag;)
                if (len[s[now][0]]>=x)
                    now=s[now][0];
                else
                {
                    x-=len[s[now][0]];
                    if (x<=sr[now]-sl[now])
                    {
                        if (x!=sr[now]-sl[now])
                            split(now,x);
                        if (x!=1)
                            now=split(now,x-1);
                        flag=0;
                    }
                    else
                    {
                        x-=sr[now]-sl[now];
                        now=s[now][1];
                    }
                }
            splay_work(now);
            //delete
            fa[s[now][0]]=fa[s[now][1]]=0;
            if (s[now][0]==0)
                root=s[now][1];
            else
            {
                ll t;
                //t temp
                for (t=s[now][0];s[t][1]!=0;t=s[t][1])
                    ;
                splay_work(t);
                update(root=fa[s[t][1]=s[now][1]]=t);
            }
            return sl[now];
        }
        
        ll push_back(ll x)
        {
            //push back number x
            ll ans=insert(x,x+1);
            if (root==0)
                return (root=ans);
            else
            {
                ll now;
                for (now=root;s[now][1]!=0;now=s[now][1])
                    ;
                splay_work(now);
                update(fa[s[now][1]=ans]=now);
                return ans;
            }
        }
    };
    
    splay sp[300000+1];
    
    void main()
    {
        ll n,m,q;
        scanf("%lld%lld%lld",&n,&m,&q);
        size=0;
        for (ll i=1;i<=n;i++)
            sp[i].pr((i-1)*m+1,i*m);
        sp[0].pr(m,m+1);
        for (ll i=2;i<=n;i++)
            sp[0].push_back(i*m);
        for (ll i=1;i<=q;i++)
        {
            ll x,y,temp;
            scanf("%lld%lld",&x,&y);
            sp[x].push_back(sp[0].pop(x));
            printf("%lld\n",temp=sp[x].pop(y));
            sp[0].push_back(temp);
        }
    }
};

int main()
{
    dts::main();
}

纯树状数组解法 6500MS过的，最慢的点是1000MS，应该是稳的。

pre：\ 这最后的20%确实挺有难度的，有不少的细节，如果我是去正式比赛，我应该还是拿前80%稳妥一点...

然后写完瞅了眼大家的题解，呃，思路应该是差不多的，不过可能有几份题解讲的还不够详细。这里稍微总结一下。

main：\ 看到题目首先想100%的做法，想10分钟，一点思路都没有，开始看局部分。

测试点1 - 6 30%

完全是送分，直接暴力就行了，这个就不详细说了

测试点7 - 10 20%

n和m增大，存不下这么多数据了。一开始我没什么思路，先想的后面的数据，不过后面想完，回过头一下就想出来了，为了使得大家更好理解为什么会这样，大家可以先看下面。

测试点11 - 16 30%

15和16 2个点就n变大了而已，由于x = 1，所以除了第一行，后面的n全是浪费空间，根本不用管的，所以11 - 16测试点完全可以用同一个算法。

那么仔细观察这个列队操作，我们发现，会产生变化的只有第一行和最后一列。

先考虑这个最后一列，把它单独拿出来，对于每次操作，相当于把这个一列的最上面这个数字丢到第一行，然后把删掉的这个数字给插入到这一列的末尾。

仔细想想，这不就一队列的基本操作么？？先进先出，所以直接拿一个队列维护这一列就好了。

然后考虑怎么维护这一行，有点麻烦，如果我们暴力，查询是O（1），修改是O（n），如果改成链表，反过来，总复杂度还是O（qn），太大了。

我们猜，应该可以有查询和修改都是log级别的做法。又是线段，然后很自然的想到线段树和树状数组，或者一些查找树之类的。

一开始我想到的是，拿树状数组维护差分数组搞，搞了一会没法推公式，放弃这个想法了。

然后刚好想到CF上以前做过的一道题！发现两者是一样的\ CF-978C

原本的操作（1,4）表示删除第1行第4个数字，我们把它的含义稍微修改一下，操作（1,4）表示，删除第1行第4个还未被删除的数字。

这样想有什么用呢？我们拿一个数组，一开始都是1，表示没删除，删除以后改成0（这部分是单点修改），然后，前缀和（这部分是区间修改）等于4的点是不是就我们要的答案？而且可以很轻松的想到，这个点有且仅有一个。

显然这个前缀和是单调不减的，因此直接可以2分找到那个位置！！

单点修改，区间查询，树状数组基本操作，加上二分，复杂度qlogmlogm！，这部分分到手了！

然后回过头想7 - 10测试点，显然右边那一列我们得单独拿出来讨论，这在刚才我们已经发现了，因为这一列很特别。

然后我们发现有个突破口，之前n很大 x = 1，然后很多数字完全不会被访问到，因此省了空间，那这里是不是也可以通过类似的办法省空间呢？

废话，当然可以，突然发现q太小了，才500，撑死500行会发生修改，你只需要开500 * 50000的数组就完事了。

你需要离线处理，然后直接离散一下（记得记录行号之间的映射关系），只存存在修改的那几列就行了，然后最后一列单独拿粗来暴力维护。

整个算法还是暴力的，因此这部分可以跟1 - 6一起做，总复杂度应该是q（n + m），没有压力。

80分很快就到手了，想加写程序都很轻松，1小时不到就完成了，下面贴一下80分的源码。觉得有困难的可以先练练手（注意开long long，还有强转）

#include <stdio.h>
#include <vector>
#include <algorithm>
#include <string.h>
#include <limits.h>
#include <string>
#include <iostream>
#include <queue>
#include <math.h>
#include <map>
#include <stack>
#include <set>
#include <complex>
#define left (now<<1)
#define right ((now<<1)+1)
#define mid ((l + r) >> 1)
#define midmid ((r + mid) >> 1)
#define LONG_LONG_MIN -9223372036854775808ll
#define LONG_LONG_MAX 9223372036854775807ll
using namespace std;
typedef long long int ll;

const int MAXN = 3e5 + 10;

struct s1{
int x,y;
};

int n,m,q,nn;
queue<ll> qq;
s1 a[MAXN];
int bit[2 * MAXN],len;
ll data[2 * MAXN];
bool flag;
ll g[510][50010];
int pos[50010];

int lowbit(int x){
return x & (-x);
}

void add(int x,int y){
while(x <= 600000){
bit[x] += y; x += lowbit(x);
}
}

int getsum(int x){
int re = 0;
while(x > 0){
re += bit[x]; x -= lowbit(x);
}
return re;
}

int main(){
scanf("%d%d%d",&n,&m,&q); flag = true;
for(int i = 1; i <= q; ++i){
scanf("%d%d",&a[i].x,&a[i].y);
if(a[i].x != 1){
flag = false;
}
}
if(flag){
for(int i = 2; i <= n; ++i){
qq.push(1ll * i * m);
}
for(int i = 1; i <= 600000; ++i){
bit[i] = lowbit(i);
}
len = m;
for(int i = 1; i <= m; ++i){
data[i] = i;
}
for(int i = 1; i <= q; ++i){
int l,r; l = 1; r = len;
while(l < r){
if(getsum(mid) >= a[i].y){
r = mid;
}else{
l = mid + 1;
}
}
printf("%lld\n",data[l]); add(l,-1); qq.push(data[l]);
data[++len] = qq.front(); qq.pop();
}

}else{
if(q <= 500){
for(int i = 1; i <= n; ++i){
data[i] = 1ll * m * i;
pos[i] = 0;
}
nn = 0;
for(int i = 1; i <= q; ++i){
if(pos[a[i].x] == 0){
pos[a[i].x] = ++nn;
for(int j = 1; j <= m - 1; ++j){
g[nn][j] = 1ll * (a[i].x - 1) * m + j;
}
}
}
for(int i = 1; i <= q; ++i){
ll x = a[i].x; ll xx = pos[a[i].x];
if(a[i].y != m){
ll ans = g[xx][a[i].y];
printf("%lld\n",ans);
for(int j = a[i].y; j < m - 1; ++j){
g[xx][j] = g[xx][j + 1];
}
g[xx][m - 1] = data[x];
for(int j = x; j < n; ++j){
data[j] = data[j + 1];
}
data[n] = ans;
}else{
ll ans = data[x];
printf("%lld\n",ans);
for(int j = x; j < n; ++j){
data[j] = data[j + 1];
}
data[n] = ans;
}
}
}else{
return 0;
}
}
return 0;
}
好了，80分到手了，现场的话，1小时T3拿了80还是很舒服的，但是我们现在肯定不满足于只拿80分，剩下20分怎么搞？？

一般前面的数据点都会对正解有提示性，就跟数学考试，前几问一般会对最后一问有提示性作用。

我们想下刚才整理的思路。

首先最后一列肯定单独拿出来维护，我们发现，这个时候这个最后一列是删一个点，然后尾部插入，这不就是咱们11 - 16的第一行的算法么？？

直接拿那部分算法的思路维护这一列就OK了，easy

然后是空间的问题，考虑到我们之前的思路，因为q比起n * m来说，太小太小了，很多点直接仍然是原先的相邻关系，一块一块的。而且之前我们是靠离线处理（预先读入q）来搞一些事，把空间省下来，这里很可能就是类似的办法。

想到这里还算轻松，后面我就想的有点慢了，因为解法不太清晰。

由于每次对某行修改，这一行和最后特别的那一列有互动，除此之外跟其他行根本不会有任何影响。因此考虑，把某一行的操作都单独取出来，看看能不能搞点事。

然后我就立马想到了做法

假设现在都是对第i行操作，一行有m个，操作按顺序为2,2,4

按我们刚才的想法，你去删了2，后面2个操作就变成实际删第3个数，和第5个数，这部分也可以拿树状数组搞诶，跟最后一列是一样的。

那么我们把每一行的操作这样单独取出来，然后算出来它的真实删的第几个数字就好了。

但是还有个很大的问题，如果算出来真实要删的数字大于等于m怎么办？？？

先想等于m的，等于m的时候，其实就是删最后一列去了。这个时候其实跟这一行木有关系，只跟当前这一列的状态有关，那么直接去这一列上搞事就好了，我们就标记一个flag，表示这个是直接在列上搞事，不需要算真实是删第几个数字。

那么大于m呢（假如是第h个）？显然，删的数字是从那一列第h - （m - 1）次加进来的。

这里我们发现q很小，也就是说对于所有的行来说，加进来的数字不超过q个（其实就是q个）,那我们可以拿一个邻接表（vector就很好~）来存第i行后面加进来的数字。

那么我们满分的算法就粗来了，我们总结下。

首先你把所有操作读进来，然后按行排序，同一行按操作先后排序，然后预处理出它真实删除的位置，如果是第m位，flag记一下，不是就算真实位置。

算完以后按编号重新排序，然后我们开始操作。

如果这个操作的y小于m，直接可以算出答案，答案就是（x - 1） * m + y 然后去维护那一列，删掉那一列第x大的数字，丢到vector<x>里，把答案插到那一列末尾

如果这个操作等于m，那么就只在列上搞事就好了，vector也不用丢。

如果大于m，先减去m（vector是从0开始的），答案就是vector[x][m]， 然后去维护最后一列，删掉第x大的数字........这部分不重述了

然后就AC啦~~~

这里有个细节，其实这个细节困扰我20，30分钟，我看题解很多人也是用别的办法搞的

就是你预处理每一行的询问的时候，每次树状数组处理完，你都得初始化，初始化的复杂度最坏是n * 3E5，肯定超时。 如果你开n个树状数组，空间必爆

所以题解很多人开了动态加点的线段树，呃

其实这里后来仔细想了想，q不是很少么，每次操作完以后，记一下，你把哪些点单点修改为0了，重新把那些点+1就好了啊、

这里记不能开bool数组记，不然枚举哪些被改了还是要平方复杂度。

搞个vector记就好了。

下面是参考代码：

#include <stdio.h>
#include <vector>
#include <algorithm>
#include <string.h>
#include <limits.h>
#include <string>
#include <iostream>
#include <queue>
#include <math.h>
#include <map>
#include <stack>
#include <set>
#include <complex>
#define left (now<<1)
#define right ((now<<1)+1)
#define mid ((l + r) >> 1)
#define midmid ((r + mid) >> 1)
#define LONG_LONG_MIN -9223372036854775808ll
#define LONG_LONG_MAX 9223372036854775807ll
using namespace std;
typedef long long int ll;

const int MAXN = 3e5 + 10;

struct s1{
int x,y,id;
bool flag;
};

vector<ll> v[MAXN];
vector<int> a;
int n,m,q,len,len2,st,ed;
s1 g[MAXN];
ll p[2 * MAXN];
int bit1[2 * MAXN],bit2[2 * MAXN];

int lowbit(int x){
return x & (-x);
}

void add(int x,int y,int *bit){
while(x <= 600010){
bit[x] += y; x += lowbit(x);
}
}

int getsum(int x,int *bit){
int re = 0;
while(x > 0){
re += bit[x]; x -= lowbit(x);
}
return re;
}

bool cmp1(s1 x,s1 y){
if(x.x != y.x){
return x.x < y.x;
}else{
return x.id < y.id;
}
}

bool cmp2(s1 x,s1 y){
return x.id < y.id;
}

int main(){
scanf("%d%d%d",&n,&m,&q); len = n;
for(int i = 1; i <= q; ++i){
scanf("%d%d",&g[i].x,&g[i].y);
g[i].id = i; g[i].flag = false;
}
for(int i = 1; i <= n; ++i){
p[i] = 1ll * i * m;
}
for(int i = 1; i <= 600010; ++i){
bit1[i] = bit2[i] = lowbit(i);
}
sort(g + 1,g + 1 + q,cmp1); st = 1; ed = 1;
while(st <= q){
while(ed < q && g[st].x == g[ed + 1].x){
++ed;
}
a.clear(); len2 = m;
for(int i = st; i <= ed; ++i){
if(g[i].y == m){
g[i].flag = true; continue;
}
int l = 1,r = len2;
while(l < r){
if(getsum(mid,bit2) >= g[i].y){
r = mid;
}else{
l = mid + 1;
}
}
add(l,-1,bit2); a.push_back(l); g[i].y = l; ++len2;
}
for(int i = 0; i < a.size(); ++i){
add(a[i],1,bit2);
}
st = ed + 1;
}
sort(g + 1,g + 1 + q,cmp2);

for(int i = 1; i <= q; ++i){
ll ans;
if(!g[i].flag){
if(g[i].y < m){
ans = 1ll * (g[i].x - 1) * m + g[i].y;
printf("%lld\n",ans);
}else{
g[i].y = g[i].y - m;
ans = v[g[i].x][g[i].y];
printf("%lld\n",ans);
}
}

int l = 1,r = len;
while(l < r){
if(getsum(mid,bit1) >= g[i].x){
r = mid;
}else{
l = mid + 1;
}
}
add(l,-1,bit1);
if(!g[i].flag){
v[g[i].x].push_back(p[l]);
}else{
ans = p[l];
printf("%lld\n",ans);
}
p[++len] = ans;
}
return 0;
}

原文地址：NOIP2017提高组DAY2题解

考察知识：树状数组，平衡树，模拟

算法难度：XXXX+ 实现难度：XXXX+

分析：

我们先分析一下列队的移动：

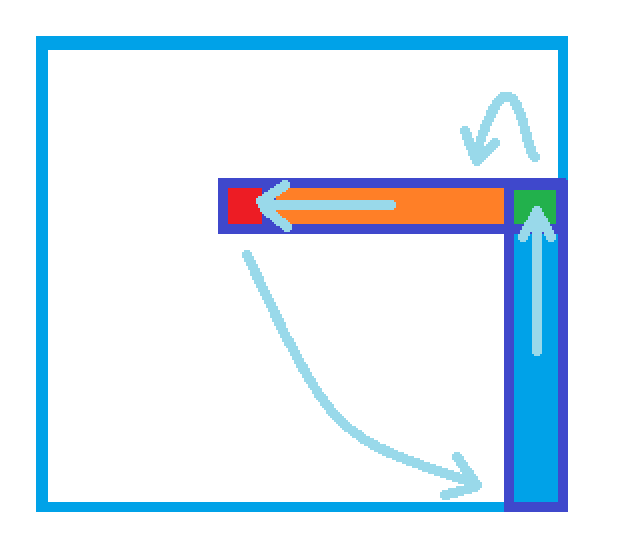
如图，我们发现如果红色那块要出队，共需要移动四块。我们发现种序列的移动可以用Splay来维护，仔细观察发现，水平有n行可能需要移动，而竖直只可能发生在最后一列，所以我们维护 n+1 个Splay，维护n个长度为m-1的序列，1个长度为n的序列。

每次移动时（x,y），我们需要将水平第x个Splay中第y个元素删除，将竖直Splay的第x个元素删除，然后将删除的两个元素分别插入这两个Spaly就可以了。

但是如果我们直接开Splay，空间不够，注意到，我们可以用Spaly维护区间，每次删除时需要将区间一分为三，然后将中间元素删除并更新剩余两个区间。

理解了上面的思路后，剩下的就基本是Spaly的基本操作+变形了，考察大家对Splay的熟练程度了。

注意：

1.最大值会超过int，所以区间用long long储存

2.Spaly常数比较大，可能会有部分点超时。（vijos：可以AC；洛谷：不开O2 95 开O2 AC）

代码：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
const int N=300005,maxn=2400005;
int ch[maxn][2],fa[maxn],sz[maxn],now,cnt[maxn];
ll L[maxn],R[maxn];
struct Splay{
    int rt;
    Splay(){rt=0;} 
    int NewNode(ll l,ll r){//新建节点 
        now++,L[now]=l,R[now]=r;
        sz[now]=cnt[now]=r-l+1;
        return now;
    }
    void init(ll l,ll r){rt=NewNode(l,r);}//空树的初始化 
    #define upd(x) cnt[x]=R[x]-L[x]+1
    #define pushup(x) sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x]
    #define DB_ for(int i=0;i<=now;i++) \
    printf("[%lld,%lld]%d<- %d[%lld,%lld] ->%d[%lld,%lld]\n", \
    L[ch[i][0]],R[ch[i][0]],ch[i][0],i,L[i],R[i],ch[i][1],L[ch[i][1]],R[ch[i][1]]);\
    puts("----------------")
    int chk(int x){return x==ch[fa[x]][1];}
    void rotate(int x){
        int y=fa[x],z=fa[y],k=chk(x),w=ch[x][k^1];
        ch[y][k]=w,fa[w]=y;
        ch[z][chk(y)]=x,fa[x]=z;
        ch[x][k^1]=y,fa[y]=x;
        pushup(y),pushup(x);
    }
    void splay(int x,int goal=0){
        while(fa[x]!=goal){
            int y=fa[x],z=fa[y];
            if(z!=goal){
                if(chk(x)==chk(y)) rotate(y);
                else rotate(x);
            } rotate(x);
        } if(!goal) rt=x;
    }
    void insert(ll l,ll r){//插入到序列末尾 
        if(rt==0) {init(l,r);return;}
        int cur=rt;
        while(ch[cur][1]) cur=ch[cur][1];
        ch[cur][1]=NewNode(l,r),fa[ch[cur][1]]=cur;
        splay(ch[cur][1]);
    }
    int beside(int x,int pre){//求一个子序列的前驱/后继 
        splay(x);
        int cur=ch[x][pre^1];
        if(!cur) return 0;
        while(ch[cur][pre]) cur=ch[cur][pre];
        return cur;
    }
    ll kth_and_del(int k,bool exit_=false){//查找第k大的数并从子序列中删除 
        int cur=rt;
        if(sz[rt]==1){//只有一个数 
            rt=0;//变为空树 
            return L[cur];
        }
        while(true){//kth
            if(ch[cur][0]&&k<=sz[ch[cur][0]])
              cur=ch[cur][0];
            else if(k>sz[ch[cur][0]]+cnt[cur])
              k-=sz[ch[cur][0]]+cnt[cur],cur=ch[cur][1];
            else break;
        }
        k-=sz[ch[cur][0]];
        if(exit_) return L[cur]+k-1;//仅查询不删除，用于查看中间结果 
        int pre=beside(cur,1),nxt=beside(cur,0);//del
        if(pre) splay(pre);
        if(nxt) splay(nxt,pre);
        if(L[cur]==R[cur]){//子序列只有一个数，直接删除 
            if(nxt) ch[nxt][0]=0;//特别注意！分类讨论不存在前驱或后继的情况 
            else if(pre) ch[pre][1]=0;
            else rt=0; 
            if(pre) sz[pre]--;
            if(nxt) sz[nxt]--;
            return L[cur];
        }
        else{
            ll ret=L[cur]+k-1;
            if(k==1) L[cur]++,upd(cur),sz[cur]--;
            else if(k==cnt[cur]) R[cur]--,upd(cur),sz[cur]--;
            else{//将子序列一分为三，并删除中间的数 
                ch[cur][0]=NewNode(L[cur],L[cur]+k-2); 
                fa[ch[cur][0]]=cur;
                L[cur]+=k,upd(cur),pushup(cur);
                splay(cur);
            }
            return ret;
        }
    }
}s[N];
int n,m,q;
void build(){
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++)
      s[i].init((ll)(i-1)*m+1,(ll)i*m-1);
    s[0].init((ll)m,(ll)m);
    for(int i=2;i<=n;i++)
      s[0].insert((ll)i*m,(ll)i*m);
}
void solve(){
    int x,y;
    ll last=(ll)n*m;
    while(q--){
        scanf("%d%d",&x,&y);
        if(y!=m){
            ll t1=s[x].kth_and_del(y),t2=s[0].kth_and_del(x);
            printf("%lld\n",last=t1);
            s[x].insert(t2,t2);
            s[0].insert(t1,t1);
        } else if(x!=n){
            ll t=s[0].kth_and_del(x);
            printf("%lld\n",last=t);
            s[0].insert(t,t);
        }else{
            printf("%lld\n",last);
        }
//      DB_; //用于查看当前各Splay节点情况 
    }
}
int main(){
    build();
    solve();
    return 0;
}

#include <stdio.h>
#include <vector>
#include <algorithm>
#include <string.h>
#include <limits.h>
#include <string>
#include <iostream>
#include <queue>
#include <math.h>
#include <map>
#include <stack>
#include <set>
#include <complex>
#define left (now<<1)
#define right ((now<<1)+1)
#define mid ((l + r) >> 1)
#define midmid ((r + mid) >> 1)
#define LONG_LONG_MIN -9223372036854775808ll
#define LONG_LONG_MAX 9223372036854775807ll
using namespace std;
typedef long long int ll;

const int MAXN = 3e5 + 10;

struct s1{
int x,y,id;
bool flag;
};

vector<ll> v[MAXN];
vector<int> a;
int n,m,q,len,len2,st,ed;
s1 g[MAXN];
ll p[2 * MAXN];
int bit1[2 * MAXN],bit2[2 * MAXN];

int lowbit(int x){
return x & (-x);
}

void add(int x,int y,int *bit){
while(x <= 600010){
bit[x] += y; x += lowbit(x);
}
}

int getsum(int x,int *bit){
int re = 0;
while(x > 0){
re += bit[x]; x -= lowbit(x);
}
return re;
}

bool cmp1(s1 x,s1 y){
if(x.x != y.x){
return x.x < y.x;
}else{
return x.id < y.id;
}
}

bool cmp2(s1 x,s1 y){
return x.id < y.id;
}

int main(){
scanf("%d%d%d",&n,&m,&q); len = n;
for(int i = 1; i <= q; ++i){
scanf("%d%d",&g[i].x,&g[i].y);
g[i].id = i; g[i].flag = false;
}
for(int i = 1; i <= n; ++i){
p[i] = 1ll * i * m;
}
for(int i = 1; i <= 600010; ++i){
bit1[i] = bit2[i] = lowbit(i);
}
sort(g + 1,g + 1 + q,cmp1); st = 1; ed = 1;
while(st <= q){
while(ed < q && g[st].x == g[ed + 1].x){
++ed;
}
a.clear(); len2 = m;
for(int i = st; i <= ed; ++i){
if(g[i].y == m){
g[i].flag = true; continue;
}
int l = 1,r = len2;
while(l < r){
if(getsum(mid,bit2) >= g[i].y){
r = mid;
}else{
l = mid + 1;
}
}
add(l,-1,bit2); a.push_back(l); g[i].y = l; ++len2;
}
for(int i = 0; i < a.size(); ++i){
add(a[i],1,bit2);
}
st = ed + 1;
}
sort(g + 1,g + 1 + q,cmp2);

for(int i = 1; i <= q; ++i){
ll ans;
if(!g[i].flag){
if(g[i].y < m){
ans = 1ll * (g[i].x - 1) * m + g[i].y;
printf("%lld\n",ans);
}else{
g[i].y = g[i].y - m;
ans = v[g[i].x][g[i].y];
printf("%lld\n",ans);
}
}

int l = 1,r = len;
while(l < r){
if(getsum(mid,bit1) >= g[i].x){
r = mid;
}else{
l = mid + 1;
}
}
add(l,-1,bit1);
if(!g[i].flag){
v[g[i].x].push_back(p[l]);
}else{
ans = p[l];
printf("%lld\n",ans);
}
p[++len] = ans;
}
return 0;
}