//好题~
//首先为了方便处理，把四个角上的点加入，再按横坐标进行排序
//根据贪心的原理，最大子矩形的四边要么贴着边界，要么贴着某些点。这样
//的话，当左边界确定后，完全可以从左到右遍历，每次更新上下边界和答案
//
//但这样的话会有遗漏的点，需要再从右向左反着再找一次，还有就是要按纵
//坐标排序，直接更新两端顶着左右边界情况
#include<iostream>
#include<algorithm>
using namespace std;
struct node{
    int x,y;
}q[5010];
int cmp(const node&x,const node&y)
{
    if(x.x!=y.x)
     return x.x<y.x;
    return x.y<y.y;
}
int cmp2(const node&x,const node&y)
{
    return x.y<y.y;
}

int main()
{
    int n,i,j,l,w,up,down,maxn=0;
    cin>>l>>w>>n;
    for(i=1;i<=n;i++)
     cin>>q[i].x>>q[i].y;
    q[n+1].x=l;
    q[n+1].y=w;
    q[n+2].x=l;
    q[n+2].y=0;
    q[n+3].x=0;
    q[n+3].y=w;
    q[n+4].x=0;
    q[n+4].y=0;
    n+=4;
    sort(q+1,q+n+1,cmp);
    for(i=1;i<=n;i++)
    {
        up=w;
        down=0;
        for(j=i+1;j<=n;j++)
        {
            maxn=max(maxn,(q[j].x-q[i].x)*(up-down));
            if(q[j].y==q[i].y)
             break;
            if(q[j].y>q[i].y)
             up=min(up,q[j].y);
            if(q[j].y<q[i].y)
             down=max(down,q[j].y);
        }
    }
    for(i=n;i>0;i--)
    {
        up=w;
        down=0;
        for(j=i-1;j>0;j--)
        {
            maxn=max(maxn,(q[i].x-q[j].x)*(up-down));
            if(q[j].y==q[i].y)
             break;
            if(q[j].y>q[i].y)
             up=min(up,q[j].y);
            if(q[j].y<q[i].y)
             down=max(down,q[j].y);
        }
    }
    sort(q+1,q+n+1,cmp2);
    for(i=2;i<=n;i++)
     maxn=max(maxn,(q[i].y-q[i-1].y)*l);
    cout<<maxn;
    return 0;
}

极大化思想......

#include <stdio.h>
#include <algorithm>
using namespace std;
const int maxn=5005;

int ans;
int l,w,n;
struct node{int x,y;}e[maxn];
inline bool cp1(node a,node b){return a.x<b.x;}
inline bool cp2(node a,node b){return a.y<b.y;}

int main()
{
    scanf("%d%d%d",&l,&w,&n);
    for(int i=1;i<=n;i++)
        scanf("%d%d",&e[i].x,&e[i].y);
    e[++n].x=0,e[n].y=0;
    e[++n].x=0,e[n].y=w;
    e[++n].x=l,e[n].y=0;
    e[++n].x=l,e[n].y=w;
    sort(e+1,e+n+1,cp1);
    for(int i=1;i<n;i++)
    {
        int u=w,d=0;
        for(int j=i+1;j<=n;j++)
        {
            if(e[j].y>=d && e[j].y<=u)
            {
                ans=max(ans,(e[j].x-e[i].x)*(u-d));
                if(e[j].y>e[i].y) u=e[j].y;
                else d=e[j].y;
            }
            if(u==d) break;
        }
    }
    sort(e+1,e+n+1,cp2);
    for(int i=1;i<n;i++)
    {
        int u=0,d=l;
        for(int j=i+1;j<=n;j++)
        {
            if(e[j].x>=u && e[j].x<=d)
            {
                ans=max(ans,(e[j].y-e[i].y)*(d-u));
                if(e[j].x>e[i].x) d=e[j].x;
                else u=e[j].x;              
            }
            if(u==d) break;
        }
    }
    printf("%d",ans);
    return 0;
}

论文中2中特殊情况的解决方法：
当左边界为0时，无须判断Y坐标大小，直接分成上部分和下部门继续计算，我用了递归。。
var
i,j,k,m,n,a1,a2,l,w,b1,b2,ans:Longint;
x,y:array[0..15001]of longint;
procedure go(k,u,d,l:Longint);
var
r:longint;
begin
if k>n then exit;
r:=x[k];
if (r=l) then begin go(k+1,u,d,l);exit;end;
if (r-l)*(u-d)>ans then ans:=(r-l)*(u-d);
if (u<=y[k])or(d>=y[k]) then begin go(k+1,u,d,l);exit;end;
×× if (y[k]>y[i])or(l=0) then go(k+1,y[k],d,l);××
××if (y[k]<y[i])or(l=0) then go(k+1,u,y[k],l);××

end;
procedure ins(a,b:Longint);
begin
inc(n);
x[n]:=a;
y[n]:=b;
end;
procedure first;
begin
ins(0,0);
ins(0,w);
ins(l,0);
ins(l,w);
end;
begin
read(l,w,n);
for i:=1 to n do
read(x[i],y[i]);
first;
for i:=1 to n do
for j:=i+1 to n do
if (x[i]>x[j])or((x[i]=x[j])and(y[i]<y[j])) then
begin
k:=x[i];x[i]:=x[j];x[j]:=k;
k:=y[i];y[i]:=y[j];y[j]:=k;
end;
ans:=0;
for i:=1 to n do
go(i+1,w,0,x[i]);
writeln(ans);
end.

我来简单的说一下：

先枚举极大子矩形的左边界，然后从左到右依次扫描每一个障碍点，并不断修改可行的上下边界，从而枚举出所有以这个定点为左边界的极大子矩形。考虑如图2中的三个点，现在我们要确定所有以1号点为左边界的极大矩形。先将1号点右边的点按横坐标排序。然后按从左到右的顺序依次扫描1号点右边的点，同时记录下当前的可行的上下边界。

开始时令当前的上下边界分别为整个矩形的上下边界。然后开始扫描。第一次遇到2号点，以2号点作为右边界，结合当前的上下边界，就得到一个极大子矩形（如图3）。

同时，由于所求矩形不能包含2号点，且2号点在1号点的下方，所以需要修改当前的下边界，即以2号点的纵坐标作为新的下边界。第二次遇到3号点，这时以3号点的横坐标作为右边界又可以得到一个满足性质1的矩形（如图4）。

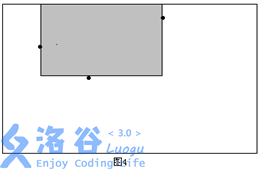
类似的，需要相应地修改上边界。以此类推，如果这个点是在当前点（确定左边界的点）上方，则修改上边界；如果在下方，则修改下边界；如果处在同一行，则可中止搜索（因为后面的矩形面积都是0了）。由于已经在障碍点集合中增加了整个矩形右上角和右下角的两个点，所以不会遗漏右边界与整个矩形的右边重合的极大子矩形（如图5）。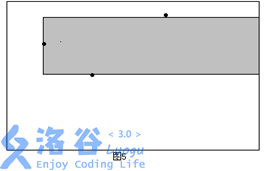

需要注意的是，如果扫描到的点不在当前的上下边界内，那么就不需要对这个点进行处理。

这样做是否将所有的极大子矩形都枚举过了呢？

可以发现，这样做只考虑到了左边界覆盖一个点的矩形，因此我们还需要枚举左边界与整个矩形的左边界重合的情况。这还可以分为两类情况。一种是左边界与整个举行的左边界重合，而右边界覆盖了一个障碍点的情况，对于这种情况，可以用类似的方法从右到左扫描每一个点作为右边界的情况。这就是上面第一个数据楼下二位错在哪里。
另一种是左右边界均与整个矩形的左右边界重合的情况，对于这类情况我们可以在预处理中完成：先将所有点按纵坐标排序，然后可以得到以相邻两个点的纵坐标为上下边界，左右边界与整个矩形的左右边界重合的矩形，显然这样的矩形也是极大子矩形，因此也需要被枚举到。

#include<cstdio>
#include<algorithm>
#include<cstring>
#define re register
#define REP(i,a,b) for (re int i=(a);i<=(b);i++)
#define DREP(i,a,b) for (re int i=(a);i>=(b);i--)
using namespace std;
const int N=5e3+7;
struct Cow{
    int x,y;
    inline bool operator < (const Cow &rhs) const {
        if (x!=rhs.x)return x<rhs.x;
        return y<rhs.y;
    }
}a[N];
int L,W,n;
inline bool cmp(Cow a,Cow b){
    return a.y<b.y;
}
inline int read(){
    re int x=0,f=1;char ch=getchar();
    while (ch<'0' || ch>'9'){if (ch=='-')f=-1;ch=getchar();}
    while ('0'<=ch && ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
    return x*f;
}
int main(){
    L=read(),W=read(),n=read();
    REP(i,1,n)a[i].x=read(),a[i].y=read();
    a[++n].x=0;a[n].y=0;
    a[++n].x=L;a[n].y=0;
    a[++n].x=0;a[n].y=W;
    a[++n].x=L;a[n].y=W;
    sort(a+1,a+n+1);
    int res=0;
    REP(i,1,n){
        re int h=W,l=0,v=L-a[i].x;
        REP(j,i+1,n)if (a[j].y<=h && a[j].y>=l){
            if (v*(h-l)<=res)break;
            res=max(res,(a[j].x-a[i].x)*(h-l));
            if (a[j].y==a[i].y)break;
            if (a[j].y>a[i].y)h=min(h,a[j].y);
            else l=max(l,a[j].y);
        }
        h=W,l=0,v=a[i].x;//王知昆dalao在此处仍将v设为l-a[i].x，这显然不对，可以自己想一想。
        DREP(j,i-1,1)
            if (a[j].y<=h && a[j].y>=l){
            if (v*(h-l)<=res)break;
            res=max(res,(a[i].x-a[j].x)*(h-l));
            if (a[i].y==a[j].y)break;
            if (a[j].y>a[i].y)h=min(h,a[j].y);
            else l=max(l,a[j].y);
        }
    }
    sort(a+1,a+n+1,cmp);
    REP(i,1,n-1)res=max(res,(a[i+1].y-a[i].y)*L);
    printf("%d",res);
    return 0;
}

//是测试数据有误吗?
//我按照 猫粮寸断的思路来写, 左右只遍历一遍, 也能AC
#include <iostream>             //最大子矩形,    (极大化思想)
#include <algorithm>
using namespace std;
const int Maxn = 5010;

int L, W, n;
int maxS = 0;

struct node {
    int i, j;
}Poi[Maxn];

bool cp_i(node a, node b) { return a.i < b.i; }

bool cp_j(node a, node b) { return a.j < b.j; }

void Scanf_Poi()
{
    for (int i = 0; i < n; i++)
        cin >> Poi[i].i >> Poi[i].j;
    Poi[n].i = 0; Poi[n].j = 0;             //插入4个角
    Poi[n + 1].i = 0; Poi[n + 1].j = W;
    Poi[n + 2].i = L; Poi[n + 2].j = 0;
    Poi[n + 3].i = L; Poi[n + 3].j = W;
    n += 4;
}

void Rectangle()
{
    int up, down;
    sort(Poi, Poi + n, cp_i);
    for (int i = 0; i < n - 1; i++)
    {
        up = W, down = 0;
        for (int j = i + 1; j < n; j++)
        {
            if (Poi[j].j >= down && Poi[j].j <= up)
            {
                maxS = max(maxS, (up - down) * (Poi[j].i - Poi[i].i));
                if (Poi[j].j < Poi[i].j)        //j点在i点下面, 更新下边届
                    down = Poi[j].j;
                else                            //否则, 更新上边届
                    up = Poi[j].j;
            }
            if (up == down)
                break;
        }
    }
    
    sort(Poi, Poi + n, cp_j);
    for (int i = 1; i < n; i++)
    {
        maxS = max(maxS, (Poi[i].j - Poi[i - 1].j) * L);
    }

}

int main()
{
    cin >> L >> W >> n;
    Scanf_Poi();
    Rectangle();
    
    cout << maxS << endl;

    system("pause");
    return 0;
}

#include <cstdio>
#include <algorithm>
using namespace std;

static const int maxm=1e6+10;

struct point{
    int x,y;
}pt[maxm];

int n,l,w,ans=-1;

bool cmp1(const point& A,const point &B){
    return A.x==B.x?A.y<B.y:A.x<B.x;
}

bool cmp2(const point &A,const point &B){
    return A.y==B.y?A.x<B.x:A.y<B.y;
}

int main(){
    scanf("%d%d%d",&l,&w,&n);
    if(!n)return printf("%d\n",l*w),0;
    for(int i=1;i<=n;i++)scanf("%d%d",&pt[i].x,&pt[i].y);

    sort(pt+1,pt+n+1,cmp1);
    
    for(int i=1;i<=n;i++){
        int u=w;int d=0;
        for(int j=i+1;j<=n;j++){
        ans=max(ans,(u-d)*(pt[j].x-pt[i].x));
        if(pt[j].y>=pt[i].y)u=min(u,pt[j].y);
        if(pt[j].y<=pt[i].y)d=max(d,pt[j].y);
        }
        ans=max(ans,(l-pt[i].x)*(u-d));
   }

    for(int i=n;i>=1;i--){
            int u=w;int d=0;
            for(int j=i-1;j>=1;j--){
            ans=max(ans,(u-d)*(pt[i].x-pt[j].x));
            if(pt[j].y>=pt[i].y)u=min(u,pt[j].y);
            if(pt[j].y<=pt[i].y)d=max(d,pt[j].y);
        }
        ans=max(ans,pt[i].x*(u-d));
    }

    sort(pt+1,pt+n+1,cmp2);

    for(int i=1;i<n;i++)
        ans=max(ans,l*(pt[i+1].y-pt[i].y));
    
    printf("%d\n",ans);
    
    return 0;
}

要特判没有产奶点的情况，不然会wa第一个点
#include<cstdio>
struct record
{
int x,y;
};
record p[5001];
bool compare1(record a,record b)
{
return a.x<b.x;
}
bool compare2(record a,record b)
{
return a.y<b.y;
}
int ans=0,u,d,m,n,k;
int main()
{
scanf("%d%d%d",&n,&m,&k);
if(!k)
{printf("%d",m*n);return 0;}
for(int i=1;i<=k;++i)
scanf("%d%d",&p[i].x,&p[i].y);
std::sort(p+1,p+k+1,compare1);
for(int i=1;i<=k;++i)
{
u=m,d=0;
for(int j=i+1;j<=k;++j)
{
ans=std::max(ans,(p[j].x-p[i].x)*(u-d));
if(p[j].y==p[i].y)
{u=d=p[i].y;break;}
else
if(p[j].y>p[i].y)
u=std::min(u,p[j].y);
else
d=std::max(d,p[j].y);
}
ans=std::max(ans,(n-p[i].x)*(u-d));
}
for(int i=k;i;--i)
{
u=m,d=0;
for(int j=i-1;j;--j)
{
ans=std::max(ans,(p[i].x-p[j].x)*(u-d));
if(p[j].y==p[i].y)
{u=d=p[i].y;break;}
else
if(p[j].y>p[i].y)
u=std::min(u,p[j].y);
else
d=std::max(d,p[j].y);
}
ans=std::max(ans,p[i].x*(u-d));
}
std::sort(p+1,p+k+1,compare2);
for(int i=1;i<k;++i)
ans=std::max(ans,(p[i+1].y-p[i].y)*n);
printf("%d\n",ans);
return 0;
}

测试数据 #0: Accepted, time = 0 ms, mem = 480 KiB, score = 10
测试数据 #1: Accepted, time = 0 ms, mem = 472 KiB, score = 10
测试数据 #2: Accepted, time = 0 ms, mem = 468 KiB, score = 10
测试数据 #3: Accepted, time = 0 ms, mem = 476 KiB, score = 10
测试数据 #4: Accepted, time = 93 ms, mem = 476 KiB, score = 10
测试数据 #5: Accepted, time = 0 ms, mem = 472 KiB, score = 10
测试数据 #6: Accepted, time = 109 ms, mem = 480 KiB, score = 10
测试数据 #7: Accepted, time = 156 ms, mem = 468 KiB, score = 10
测试数据 #8: Accepted, time = 171 ms, mem = 472 KiB, score = 10
测试数据 #9: Accepted, time = 62 ms, mem = 468 KiB, score = 10
Accepted, time = 591 ms, mem = 480 KiB, score = 100
最开始脑残了，上下边界的处理出现了问题，后来改正就AC了，或许因为我过多使用了封装的东西，导致稍稍慢了点儿吧
具体的思想就是枚举左右边界，先确定一个左边界，枚举右边界，不断地修改上下边界，这样的话一定会得到一个最大的子矩形。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 5050;
struct node{
int x, y;
bool operator < (const node &rhs)const{
return rhs.x < x;
}
};
node s[maxn];
int w, l, n;
int main(){
scanf("%d%d", &l, &w);
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d%d", &s[i].x, &s[i].y);
s[n++] = (node){0, 0}; s[n++] = (node){w, 0};
s[n++] = (node){0, l}; s[n++] = (node){w, l};
sort(s, s + n);
int left, right, up, down;
int ans = 0;
for (int i = 0; i < n; i++){
left = s[i].x; up = 0; down = l;
for (int j = i + 1; j < n; j++){
if (s[j].x == left) continue;
right = s[j].x;
int ss = abs((right - left) * (down - up));
ans = max(ans, ss);
if (s[j].y < down && s[j].y >= s[i].y){down = s[j].y;}
if (s[j].y > up && s[j].y <= s[i].y){up = s[j].y;}
if (up >= down) break;
}
}
printf("%d\n", ans);
return 0;
}

感谢 王知昆《浅谈用极大化思想解决最大子矩形问题》 给我的指导！

极大化思想

先排序

把4个顶点加上 作为边界

for(i=1;i

最大子矩形问题..

极大化思想

编译通过...

├ 测试数据 01：答案正确... 0ms

├ 测试数据 02：答案正确... 0ms

├ 测试数据 03：答案正确... 0ms

├ 测试数据 04：答案正确... 0ms

├ 测试数据 05：答案正确... 0ms

├ 测试数据 06：答案正确... 0ms

├ 测试数据 07：答案正确... 25ms

├ 测试数据 08：答案正确... 72ms

├ 测试数据 09：答案正确... 150ms

├ 测试数据 10：答案正确... 0ms

---|---|---|---|---|---|---|---|-

Accepted 有效得分：100 有效耗时：247ms

题解：

http://254117343.blog.163.com/

s表示障碍点数量，定义极大子矩形表示上下左右边界上都有障碍点。

O(s^2)做法：

分三种情况，一种是左边界在边界上且右边界不在边界上的，一种是左边界右边界都在边界上的，一种左边界上有障碍点而右边界上没有的。

对于第二种，预处理。

对于第三种，枚举左边界上的点，枚举右边界，并维护以该点为左边界上的点的极大子矩形即可。

对于第一种，类似第三种。

O(nm)做法：

定义u[i][j]表示从(i,j)往上最大能延伸的长度。l[i][j]表示以u[i][j]为宽

，以(i,j)为右下角，往左最大延伸长度。r[i][j]同l[i][j]。则l,r可以从(i-

1,j)推得。接下来枚举(i,j)，求max(u[i][j]*(l[i][j]+r[i][j]))即可

即使障碍点多，也可以离散以后用NM做法。

编译通过...

├ 测试数据 01：答案正确... 0ms

├ 测试数据 02：答案正确... 0ms

├ 测试数据 03：答案正确... 0ms

├ 测试数据 04：答案正确... 0ms

├ 测试数据 05：答案正确... 0ms

├ 测试数据 06：答案正确... 0ms

├ 测试数据 07：答案正确... 0ms

├ 测试数据 08：答案正确... 0ms

├ 测试数据 09：答案正确... 0ms

├ 测试数据 10：答案正确... 0ms

---|---|---|---|---|---|---|---|-

Accepted 有效得分：100 有效耗时：0ms

交了五六次后……过了……

学了极大化……秒杀……

晒晒……

=========================puppy的分割线=========================

program v1055;

type rec=record

x,y:longint;

end;

var a:array[0..5005] of rec;

i,j,l,w,k,u,d,s,n,temp,r:longint;

procedure qsort(s,e:longint);

var t:rec;

x,i,j:longint;

begin

i:=s; j:=e;

x:=a[random(e-s)+s].x;

repeat

while a[i].xx do dec(j);

if ij;

if is then qsort(s,j);

end;

begin

readln(l,w);

readln(n);

for i:=1 to n do

readln(a[i].x,a[i].y);

i:=n;

a[n+1].x:=0; a[n+1].y:=0;

a[n+2].x:=l; a[n+2].y:=0;

a[n+3].x:=0; a[n+3].y:=w;

a[n+4].x:=l; a[n+4].y:=w;

randomize;

qsort(1,n+4);

s:=0;

for i:=1 to n+3 do

begin

u:=0; d:=w;

for j:=i+1 to n+4 do

begin

if (a[j].x=a[i].x)or(a[j].y>d)or(a[j].ys then s:=temp;

if (a[j].y=a[i].y) then d:=a[j].y;

if (a[j].y>u)and(a[j].y=d then break;

end;

end;

writeln(s);

end.

极大化思想。。不过我的编程能力不时很强。。没有秒杀（尽管来鄙视我吧）

这里有论文的图片版：

http://hi.baidu.com/%C4%BE%D7%D3%C8%D5%D4%C8/blog/item/a441612a79790cf0e6cd4087.html

极大化思想 强！！！

编译通过...

├ 测试数据 01：答案正确... 0ms

├ 测试数据 02：答案正确... 0ms

├ 测试数据 03：答案正确... 0ms

├ 测试数据 04：答案正确... 0ms

├ 测试数据 05：答案正确... 0ms

├ 测试数据 06：答案正确... 0ms

├ 测试数据 07：答案正确... 0ms

├ 测试数据 08：答案正确... 0ms

├ 测试数据 09：答案正确... 0ms

├ 测试数据 10：答案正确... 0ms

---|---|---|---|---|---|---|---|-

Accepted 有效得分：100 有效耗时：0ms

orz WZK

Accepted 有效得分：100 有效耗时：146ms

一开始想到一个s^3的算法没敢写,不知道会不会超......

看完WC2003WZK的论文后---|1次AC(好爽)!

强大的极大化矩阵.s^2

郁闷，小错误不断，快排的时候注意别调用错程序.....

这题障碍点才5000个，当然选(s^2)啦。(N*M)反倒更大。

样例？