#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <queue>
using namespace std;
 
const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
    if(Head == Tail) {
        int l = fread(buffer, 1, BufferSize, stdin);
        Tail = (Head = buffer) + l;
    }
    return *Head++;
}
int read() {
    int x = 0, f = 1; char c = Getchar();
    while(!isdigit(c)){ if(c == '-') f = -1; c = Getchar(); }
    while(isdigit(c)){ x = x * 10 + c - '0'; c = Getchar(); }
    return x * f;
}
 
#define maxn 100010
#define maxnode 1000010
#define maxm 6000380
#define maxlog 17
#define ool (1ll << 60)
#define LL long long
 
namespace NG {
    int ToT, val[maxnode];
     
    int iRt[maxn], oRt[maxn];
    struct Seg_info {
        int l, r, lc, rc;
        Seg_info() {}
        Seg_info(int _1, int _2, int _3, int _4): l(_1), r(_2), lc(_3), rc(_4) {}
    } info[maxnode];
     
    int m, head[maxnode], nxt[maxm], to[maxm], dist[maxm];
    void init() {
        ToT = 0;
        memset(val, 0, sizeof(val));
        m = 0; memset(head, 0, sizeof(head));
        return ;
    }
     
    void AddEdge(int a, int b, int c) {
//      printf("NG::AddEdge(%d -> %d : %d)\n", a, b, c);
        to[++m] = b; dist[m] = c; nxt[m] = head[a]; head[a] = m;
        return ;
    }
     
    int iseg_node(int o, int pos) {
        if(info[o].l == info[o].r) return o;
        int mid = info[o].l + info[o].r >> 1;
        if(pos <= mid) {
            if(!info[o].lc) {
                info[o].lc = ++ToT;
                info[info[o].lc] = Seg_info(info[o].l, mid, 0, 0);
                AddEdge(info[o].lc, o, 0);
            }
            return iseg_node(info[o].lc, pos);
        }
        if(!info[o].rc) {
            info[o].rc = ++ToT;
            info[info[o].rc] = Seg_info(mid + 1, info[o].r, 0, 0);
            AddEdge(info[o].rc, o, 0);
        }
        return iseg_node(info[o].rc, pos);
    }
    int oseg_node(int o, int pos) {
        if(info[o].l == info[o].r) return o;
        int mid = info[o].l + info[o].r >> 1;
        if(pos <= mid) {
            if(!info[o].lc) {
                info[o].lc = ++ToT;
                info[info[o].lc] = Seg_info(info[o].l, mid, 0, 0);
                AddEdge(o, info[o].lc, 0);
            }
            return oseg_node(info[o].lc, pos);
        }
        if(!info[o].rc) {
            info[o].rc = ++ToT;
            info[info[o].rc] = Seg_info(mid + 1, info[o].r, 0, 0);
            AddEdge(o, info[o].rc, 0);
        }
        return oseg_node(info[o].rc, pos);
    }
     
    int cIntv, Intv[maxn];
    void getintv(int o, int ql, int qr) {
        if(!o) return ;
        if(ql <= info[o].l && info[o].r <= qr) Intv[++cIntv] = o;
        else {
            int mid = info[o].l + info[o].r >> 1;
            if(ql <= mid) getintv(info[o].lc, ql, qr);
            if(qr > mid) getintv(info[o].rc, ql, qr);
        }
        return ;
    }
    void GetIntv(int o, int ql, int qr) {
        cIntv = 0;
        if(ql > qr) return ;
        getintv(o, ql, qr);
        return ;
    }
     
    struct Node {
        int u; LL d;
        Node() {}
        Node(int _, LL __): u(_), d(__) {}
        bool operator < (const Node& t) const { return d > t.d; }
    };
    priority_queue <Node> Q;
    bool vis[maxnode];
    LL d[maxnode];
    void ShortPath(int s) {
        memset(vis, 0, sizeof(vis));
        for(int i = 1; i <= ToT; i++) d[i] = ool;
        d[s] = 0; Q.push(Node(s, 0));
        while(!Q.empty()) {
            int u = Q.top().u; Q.pop();
//          printf("(u)%d ", u);
            if(vis[u]) continue;
            vis[u] = 1;
            for(int e = head[u]; e; e = nxt[e]) if(d[to[e]] > d[u] + dist[e] + val[to[e]]) {
                d[to[e]] = d[u] + dist[e] + val[to[e]];
                if(!vis[to[e]]) Q.push(Node(to[e], d[to[e]]));
            }
        }
        return ;
    }
}
 
struct Edge {
    int from, to, dist, tnode;
    Edge() {}
    Edge(int _1, int _2, int _3, int _4): from(_1), to(_2), dist(_3), tnode(_4) {}
} es[maxn];
struct Graph {
    int m, hto[maxn], nto[maxn], hfr[maxn], nfr[maxn];
     
    void init() { m = 0; memset(hto, 0, sizeof(hto)); memset(hfr, 0, sizeof(hfr)); return ; }
     
    void AddEdge(int a, int b, int c, int d) {
        es[++m] = Edge(a, b, c, d);
        nto[m] = hto[a]; hto[a] = m;
        nfr[m] = hfr[b]; hfr[b] = m;
        return ;
    }
} G;
 
struct Tree {
    int n, m, head[maxn], nxt[maxn], to[maxn];
    int dep[maxn], Log[maxn<<1], mnp[maxlog][maxn<<1], pos[maxn], clo;
     
    void init() { m = 0; memset(head, 0, sizeof(head)); clo = 0; return ; }
     
    void AddEdge(int a, int b) {
        to[++m] = b; nxt[m] = head[a]; head[a] = m;
        return ;
    }
     
    void build(int u) {
        mnp[0][++clo] = u; pos[u] = clo;
        for(int e = head[u]; e; e = nxt[e]) {
            dep[to[e]] = dep[u] + 1;
            build(to[e]);
            mnp[0][++clo] = u;
        }
        return ;
    }
    void rmq_init() {
        Log[1] = 0;
        for(int i = 2; i <= clo; i++) Log[i] = Log[i>>1] + 1;
        for(int j = 1; (1 << j) <= clo; j++)
            for(int i = 1; i + (1 << j) - 1 <= clo; i++) {
                int a = mnp[j-1][i], b = mnp[j-1][i+(1<<j-1)];
                mnp[j][i] = dep[a] < dep[b] ? a : b;
            }
        return ;
    }
    int lca(int a, int b) {
        int l = pos[a], r = pos[b];
        if(l > r) swap(l, r);
        int t = Log[r-l+1];
        a = mnp[t][l]; b = mnp[t][r-(1<<t)+1];
        return dep[a] < dep[b] ? a : b;
    }
    int cdist(int a, int b) {
        return dep[a] + dep[b] - (dep[lca(a,b)] << 1);
    }
} tree;
 
bool cmp(int a, int b) { return tree.pos[a] < tree.pos[b]; }
struct VTree {
    int n, m, head[maxn], nxt[maxn], to[maxn], dist[maxn];
    int nodes[maxn], iN[maxn], ci, oN[maxn], co;
    int dl[maxn], dr[maxn], clo;
    int iRt, oRt, buff[maxn], cbuff;
     
    void init() {
        m = 0; memset(head, 0, sizeof(head));
        return ;
    }
     
    void AddEdge(int a, int b, int c) {
        to[++m] = b; dist[m] = c; nxt[m] = head[a]; head[a] = m;
        return ;
    }
     
    void build(int u) {
        dl[u] = ++clo;
        for(int e = head[u]; e; e = nxt[e]) build(to[e]);
        dr[u] = clo;
        return ;
    }
     
    void AddEdges(int u) {
//      printf("AddEdgessssssssss(%d) [%d, %d] %d\n", u, dl[u], dr[u], NG::m);
        NG::GetIntv(iRt, dl[u], dl[u]);
        if(NG::cIntv) {
            int x = NG::Intv[1];
            NG::GetIntv(oRt, dl[u], dr[u]);
//          printf("[%d, %d]: %d\n", dl[u], dr[u], NG::cIntv);
            if(NG::cIntv) {
                for(int i = 1; i <= NG::cIntv; i++) {
                    NG::AddEdge(x, NG::Intv[i], tree.dep[u]);
//                  printf("HERE@@@@@@@ %d -> %d : %d\n", x, NG::Intv[i], tree.dep[u]);
                }
            }
        }
        NG::GetIntv(oRt, dl[u], dl[u]);
        if(NG::cIntv) {
            int x = NG::Intv[1];
            NG::GetIntv(iRt, dl[u] + 1, dr[u]);
            if(NG::cIntv) {
                for(int i = 1; i <= NG::cIntv; i++) {
                    NG::AddEdge(NG::Intv[i], x, tree.dep[u]);
//                  printf("HERE@@@@@@@ %d -> %d : %d | we are here %d\n", NG::Intv[i], x, tree.dep[u], u);
                }
            }
        }
        for(int e = head[u]; e; e = nxt[e]) {
            NG::GetIntv(iRt, dl[to[e]], dr[to[e]]);
            if(NG::cIntv) {
                cbuff = NG::cIntv;
                for(int i = 1; i <= cbuff; i++) buff[i] = NG::Intv[i];
            }
            else continue;
            int newnode = 0;
            NG::GetIntv(oRt, dl[u] + 1, dl[to[e]] - 1);
            if(NG::cIntv) {
                newnode = ++NG::ToT;
                for(int i = 1; i <= cbuff; i++) NG::AddEdge(buff[i], newnode, tree.dep[u]);
                for(int i = 1; i <= NG::cIntv; i++) NG::AddEdge(newnode, NG::Intv[i], 0);
            }
            NG::GetIntv(oRt, dr[to[e]] + 1, dr[u]);
            if(NG::cIntv) {
                if(newnode) for(int i = 1; i <= NG::cIntv; i++) NG::AddEdge(newnode, NG::Intv[i], 0);
                else {
                    newnode = ++NG::ToT;
                    for(int i = 1; i <= cbuff; i++) NG::AddEdge(buff[i], newnode, tree.dep[u]);
                    for(int i = 1; i <= NG::cIntv; i++) NG::AddEdge(newnode, NG::Intv[i], 0);
                }
            }
        }
        /*printf("(u)%d: ", u);
        for(int e = head[u]; e; e = nxt[e]) printf("%d ", to[e]);
        printf("to[e] ends\n");*/
        for(int e = head[u]; e; e = nxt[e]) AddEdges(to[e]);
//      printf("return to %d [%d, %d]\n", u, dl[u], dr[u]);
        return ;
    }
     
    void G_build(int u) {
        init();
        n = ci = co = 0;
        for(int e = G.hfr[u]; e; e = G.nfr[e]) iN[++ci] = e, nodes[++n] = es[e].tnode;
        for(int e = G.hto[u]; e; e = G.nto[e]) oN[++co] = e, nodes[++n] = es[e].tnode;
        if(!ci || !co) return ;
        sort(nodes + 1, nodes + n + 1, cmp);
        int t = n;
        for(int i = 1; i < t; i++) nodes[++n] = tree.lca(nodes[i], nodes[i+1]);
        sort(nodes + 1, nodes + n + 1, cmp);
        n = unique(nodes + 1, nodes + n + 1) - nodes - 1;
        for(int i = 1; i < n; i++) {
            int a = nodes[i], b = nodes[i+1], c = tree.lca(a, b);
            AddEdge(c, b, tree.cdist(c, b));
        }
        clo = 0;
        build(nodes[1]);
        NG::info[iRt = NG::iRt[u] = ++NG::ToT] = NG::Seg_info(1, clo, 0, 0);
        NG::info[oRt = NG::oRt[u] = ++NG::ToT] = NG::Seg_info(1, clo, 0, 0);
//      printf("G_build(%d) %d %d %d\n", u, n, clo, nodes[1]);
        for(int i = 1; i <= ci; i++) {
            int u = NG::iseg_node(iRt, dl[es[iN[i]].tnode]);
            NG::AddEdge(iN[i], u, 0);
        }
        for(int i = 1; i <= co; i++) {
            int u = NG::oseg_node(oRt, dl[es[oN[i]].tnode]);
            NG::AddEdge(u, oN[i], 0);
        }
        AddEdges(nodes[1]);
        return ;
    }
} vtree;
 
LL Ans[maxn];
 
void work() {
    G.init(); tree.init();
     
    int n = read(), m = read(), k = read();
//  printf("%d %d %d\n", n, m, k);
    for(int i = 1; i <= m; i++) {
        int a = read(), b = read(), c = read(), d = read();
        G.AddEdge(a, b, c, d);
    }
     
    NG::init();
    NG::ToT = m;
    for(int i = 1; i <= G.m; i++) NG::val[i] = es[i].dist;
    int Start = ++NG::ToT;
    for(int e = G.hto[1]; e; e = G.nto[e]) NG::AddEdge(Start, e, 0);
     
    for(int i = 1; i < k; i++) {
        int a = read(), b = read(); read();
        tree.AddEdge(a, b);
    }
    tree.build(1); tree.rmq_init();
     
    for(int i = 1; i <= n; i++) vtree.G_build(i);
     
//  printf("ToT: %d %d\n", NG::ToT, NG::m);
    NG::ShortPath(Start);
    for(int i = 1; i <= n; i++) Ans[i] = ool;
    for(int i = 1; i <= G.m; i++) Ans[es[i].to] = min(Ans[es[i].to], NG::d[i]);
     
    for(int i = 2; i <= n; i++) printf("%lld\n", Ans[i]);
     
    return ;
}
 
int main() {
    int T = read();
    while(T--) work();
     
    return 0;
}

这题思路的前半部分挺妙的，后半部分就丧心病狂了。。。

首先考虑暴力，我们可以把原图上的每个边作为新图的节点，这样我们最短路转移的时候就可以方便地知道上一次和这一次在 Trie 树上的 lca。但是暴力连的话显然有 n2 条边，于是考虑优化建图。

先区分好三个名词：原图指输入给出的有向图，Trie 树指的是输入给出的有根树，新图指的是算法新建的图。

对于原图中每个节点，我们把和这个节点相连的边在 Trie 树上的节点拿出来建立一棵虚树。

那么我们就可以轻易的知道以某个节点为 lca 的点对有哪些了，那么在新图中创建两个用虚树 DFS 序表示的线段树，两个线段树分别管原图中的入边和出边（把它们分别称为入线段树和出线段树）。入边在新图中对应的节点向入线段树的叶节点连边，入线段树的节点之间是自底向上连边；出线段树叶节点向新图中对应点连边，出线段数的节点是自上向下连边的。

然后对于虚树上的每个节点 u，以它为 lca 的点对就是所有 u 的两两子树之间连边，那么我们枚举 u 的儿子 son，然后就是这个 son 的子树向 u 的其他儿子的子树连边，注意在 DFS 序中，“son 的子树”是一段区间，“其他儿子的子树”是两段区间，那么就是线段树上的 logn 个区间向 2logn 的区间两两连边，我们可以建一个辅助点，把边数变成 log 而不是 log2 的。除此之外，u 本身需要向它的子树连边，它的子树也要向 u 连边。注意这一段说的连边的权值都是 u 在 Trie 树上的深度。并且提醒一下在建辅助点的时候只需要把入边的权值设成深度，出边不需要再设了，否则在跑最短路时会重复计算这个代价。

关于spfa
它死了

原因是这道题你最后建出来的图就是spfa最怂的网格图，出题人甚至只需要random数据,你就自动完成了卡spfa的任务……

dijkstra保平安

本题题解
首先简化一下并不明确的题意

给出一张有向图，每个边上有边权，以及一个字符串

一条有向路径的长度为这条路径上每个边的边权之和+按照路径的顺序将这些边上的字符串排成一列，相邻两个串的lcp长度之和。

求这种长度定义下的1号点到其他点的最短路

保证边上的所有字符串都可以被一个字典树所识别，字典树的大小不会很大

那么我们仔细看一下应该还是最短路问题，所以最后肯定还是跑一遍dijkstra解决问题，现在我们的精力应该放在如何建图上

仔细看一眼你会发现这道题点在最短路当中并没有太多用处，路径长度的计算公式是和边有关的，因此我们考虑下面一个比较显然(?或许并不)的暴力建图方式

将一个边拆成两个点，一个是入点另一个是出点，中间链接一条为这条边权值的有向边，对于两个边<a,b>,<c,d>来讲，如果b=c，那么第一个边的出点向第二个边的入点连一条权值等于两个边上字符串lcp的长度的有向边。

新建一个超级源点s，对于所有形如<1,a>的边，s向这些边的入点连一条边权为0的有向边

最后输出最短路长度的时候，对于每一个点i，枚举形如<a,i>的边，在这些边的出点的dis值中找最小值，作为这个点的最短路输出

好了翻译一下上边的鬼话就是我们把边看做点重新建一张图出来，边自己的权值拆成两个点保存在这两个点之间的边权中，然后边和边之间连边的边权就是边上字符串的lcp长度

遗憾的是上边的建图方式碰到下面这张图会直接爆炸……

恭喜你连了O(m^2)条边，然后你炸了

接下来就是奇技淫巧的优化建图时间了

如果你想了刚才那个暴力你会发现我们连了一堆边权一样的边……

因为两个字符串的lcp长度就是这两个字符串在字典树上的lca深度，因此我们可以会发现所有可能的边权种类只有O(m+k)种，因此按照刚才的暴力我们一定会连出很多边权一样的边

此时我们观察了一会这个图发现一个有趣的事实

我们把每个点周围一圈的边拉出来，按照边上字符串在字典树上的dfs序排一个序，此时我们看一看会有什么有趣的现象发生呢？

由于我们现在有了一堆按照字典序排好序的字符串，因此我们觉得这非常像后缀数组，所以我们尝试着求出相邻两个字符串的lcp长度，或者说字典树上的lca深度，或者说求出这些排好序字符串的height数组

那么我们会并不惊奇的发现一个事实，两个字符串的lcp长度就是height数组的区间最小值，区间端点为这两个字符串的位置，就像后缀数组一样的性质

如果你对后缀数组那一套足够熟练的话你会非常熟练的使用单调栈求出每一个h_{i}h
i
​ 所"管辖"(也就是它是区间最小值)的范围，然后更加熟练的使用线段树优化建图完成区间链接一条权值一样的边的操作，然后以O(mlog^2m)的复杂度做完这道题

但是啊，让我们接着想想，线段树优化建图还有优化空间吗？

当然有，答案是

前缀和/后缀和优化建图
我们依然是把每个点周围一圈的边全部拉出去按照dfs序排序，依然处理出height数组,但是，我们不再使用单调栈，而是考虑这样一种奇技淫巧

对于某一个hi
​ 来讲，在i左侧的入点可以通过不超过hi
​ 代价到达i右侧出点，同理i右侧的入点可以通过不超过hi
​ 的代价到达i右侧的出点

所以我们可以让i左侧点向i右侧点连一堆边，i右侧点向i左侧点连一堆边，当然，边权都是hi
​

此时并没有任何优化，但是假设我们只需要让i左侧点向右侧点连边，则我们可以使用这样一种奇技淫巧，我们像这样连边即可，其中上边的点是入点，底下的点是出点

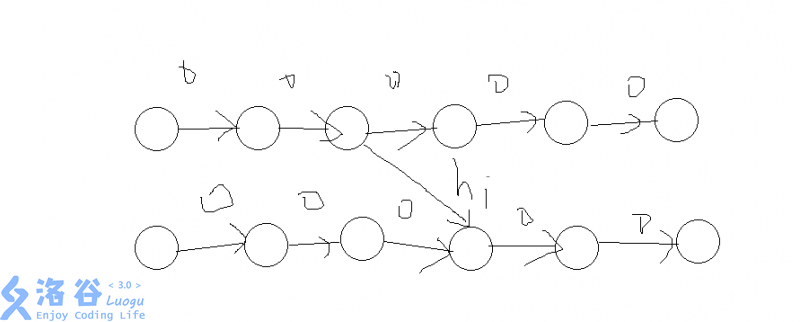
很显然我们使用了很少的边就完成了连边工作

但是用这个技巧我们并无法同时支持从左向右连和从左向右连

仔细想想真的不行吗……？

其实是可以的
我们将一条边拆成2个入点和两个出点，然后连成这样的形状

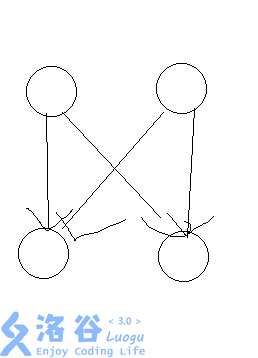
然后第一对出入点处理从左向右连的情况，第二对出入点处理从右向左的情况 即可

此时我们就可以建立一个超级源点连向1号点的所有出边跑一边dijkstra，之后对于每一个i，for一遍所有指向i的出边求最短路的最小值，然后我们就可以搞定这道题了

备注：建图会非常恶心……自己慢慢画图建吧……一不小心就写了100行……

#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
int dfn[20010];int dep[20010];int n;int m;int k;int T;typedef long long ll;
namespace Tree
{
    const int N=2*1e4+10;
    struct data{int v;int val;friend bool operator <(data a,data b){return a.val<b.val;}};
    int fa[N][18];int df;vector <data> v[N];
    inline void add(int u,int V,int w){v[u].push_back((data){V,w});}
    inline void dfs(int u)//dfs
    {
        for(int i=0;fa[u][i];i++)fa[u][i+1]=fa[fa[u][i]][i];
        dfn[u]=++df;vector <data> :: iterator it;
        for(it=v[u].begin();it!=v[u].end();++it)dep[it->v]=dep[u]+1,fa[it->v][0]=u,dfs(it->v);
    }
    inline void pre(){for(int i=1;i<=k;i++)sort(v[i].begin(),v[i].end());dfs(1);}
    inline int lca(int u,int v)//倍增lca 
    {
        if(dep[u]<dep[v])swap(u,v);
        for(int d=dep[u]-dep[v],i=0;d;d>>=1,i++)if(d&1)u=fa[u][i];if(u==v)return u;
        for(int i=17;i>=0;i--)if(fa[u][i]!=fa[v][i])u=fa[u][i],v=fa[v][i];return fa[u][0];
    }
    inline void clear()
    {
        for(int i=1;i<=k;i++)v[i].clear();
        for(int i=1;i<=k;i++)for(int j=0;j<18;j++)fa[i][j]=0;df=0;
    }
}
namespace Grph
{
    const int N=5*1e4+10;const int V=4*N;const int E=20*N;
    int tp[V];int ctt;vector <int> eif[N];vector <int> eof[N];vector <int> eib[N];vector <int> eob[N];
    vector <int> tr;int v[E];int x[E];int ct;int al[V];int val[E];int s;
    inline bool cmp(int a,int b){return dfn[tp[a]]<dfn[tp[b]];}
    inline void add(int u,int V,int w){v[++ct]=V;x[ct]=al[u];al[u]=ct;val[ct]=w;}
    inline void ins(int u,int V,int w,int d)//插入一个边 
    {
        if(u==1)add(s,ctt+1,0),add(s,ctt+3,0);for(int i=1;i<=4;i++)tp[ctt+i]=d;//拆成4条边 
        add(ctt+1,ctt+2,w);add(ctt+1,ctt+4,w);add(ctt+3,ctt+4,w);add(ctt+3,ctt+2,w);
        eof[u].push_back(++ctt);eif[V].push_back(++ctt);eob[u].push_back(++ctt);eib[V].push_back(++ctt);
    }
    inline void build()
    {
        for(int u=1;u<=n;u++)
        {
            sort(eof[u].begin(),eof[u].end(),cmp);sort(eif[u].begin(),eif[u].end(),cmp);
            sort(eob[u].begin(),eob[u].end(),cmp);sort(eib[u].begin(),eib[u].end(),cmp);
            for(int i=0;i<(int)eof[u].size()-1;i++)add(eof[u][i],eof[u][i+1],0);//将长链连出来 
            for(int i=0;i<(int)eif[u].size()-1;i++)add(eif[u][i],eif[u][i+1],0);
            for(int i=0;i<(int)eob[u].size()-1;i++)add(eob[u][i+1],eob[u][i],0);
            for(int i=0;i<(int)eib[u].size()-1;i++)add(eib[u][i+1],eib[u][i],0);
            tr.resize(eof[u].size()+eif[u].size());
            merge(eif[u].begin(),eif[u].end(),eof[u].begin(),eof[u].end(),tr.begin(),cmp);
            for(int t=0,i=0,j=0;t<(int)tr.size()-1;t++)//然后两两求lca连边 
            {
                if(tr[t]&1)j++;else i++;int w=dep[Tree::lca(tp[tr[t]],tp[tr[t+1]])];
                if(i!=0&&j!=(int)eof[u].size())add(eif[u][i-1],eof[u][j],w);
                if(i!=(int)eib[u].size()&&j!=0)add(eib[u][i],eob[u][j-1],w);
            }   
        }
    }
    struct data{int u;ll d;friend bool operator <(data a,data b){return a.d>b.d;}};
    ll d[V];bool book[V];priority_queue <data> pq;
    inline void solve()//跑dijkstra 
    {
        for(int i=1;i<=ctt;i++)d[i]=(1LL<<40);d[s]=0;
        for(pq.push((data){s,0});!pq.empty();)
        {
            data nw=pq.top();pq.pop();if(book[nw.u])continue;book[nw.u]=true;
            for(int i=al[nw.u];i;i=x[i])
                if(!book[v[i]]&&d[v[i]]>nw.d+val[i])d[v[i]]=nw.d+val[i],pq.push((data){v[i],d[v[i]]});
        }
        for(int i=2;i<=n;i++)
        {
            ll ret=(1LL<<40);for(int j=0;j<(int)eif[i].size();j++)ret=min(ret,d[eif[i][j]]);
            for(int j=0;j<(int)eib[i].size();j++)ret=min(ret,d[eib[i][j]]);printf("%lld\n",ret);
        }
    }
    inline void clear()
    {
        for(int i=1;i<=n;i++)eif[i].clear();
        for(int i=1;i<=n;i++)eof[i].clear();
        for(int i=1;i<=n;i++)eib[i].clear();
        for(int i=1;i<=n;i++)eob[i].clear();
        for(int i=1;i<=ctt+1;i++)al[i]=0;
        for(int i=1;i<=ctt+1;i++)book[i]=false;ct=0;ctt=0;
    }
}
inline void solve()
{
    scanf("%d%d%d",&n,&m,&k);Grph::s=4*m+1;
    for(int i=1,u,v,w,d;i<=m;i++)scanf("%d%d%d%d",&u,&v,&w,&d),Grph::ins(u,v,w,d);
    for(int i=1,u,v,w;i<k;i++)scanf("%d%d%d",&u,&v,&w),Tree::add(u,v,w);
    Tree::pre();Grph::build();Grph::solve();
}
inline void clear(){Tree::clear();Grph::clear();}
int main(){
    scanf("%d",&T);
    for(int z=1;z<=T;z++)solve(),clear();
    return 0;
}//拜拜程序~