题意简述

题目链接

Vijos ETO P1003

题目描述

给定一个 \(N\times N(N\le3\times10^3)\) 的网格 \(a\)。

一个商人要从左上角进（ 一开始未在左上角 ），右下角出，且不能对角穿过小方格。

穿越中间的 \(1\) 个方格需要花费 \(1\) 个单位时间，且需要缴纳一定的费用。

商人需要在 \(2N-1\) 的时间内穿越出去，且要求 最小化 需要缴纳的费用。

样例 #1

样例输入 #1

5
1  4  6  8  10
2  5  7  15 17
6  8  9  18 20
10 11 12 19 21
20 23 25 29 33

样例输出 #1

109

样例解释 #1

样例中，最小值为 \(109=1+2+5+7+9+12+19+21+33\)。

思路分析

挖掘性质

与 摘花生 一题最大的不同之处是， 时间有了限制。

这个时间到底有什么意义呢？这是需要做题人来自己分析的。

而且，我们必须找到一个性质。 如果能向左或向上走，那么就会有后效性（即后面的状态会影响前面的状态），那么就无法使用 DP 来解决问题了。

摘花生中是怎么走的？那题中是只能向右或者向下走， 无后效性。那么，*这个时间的限制会不会是让我们只能往右和往下走呢*？

我们可以验证一下。

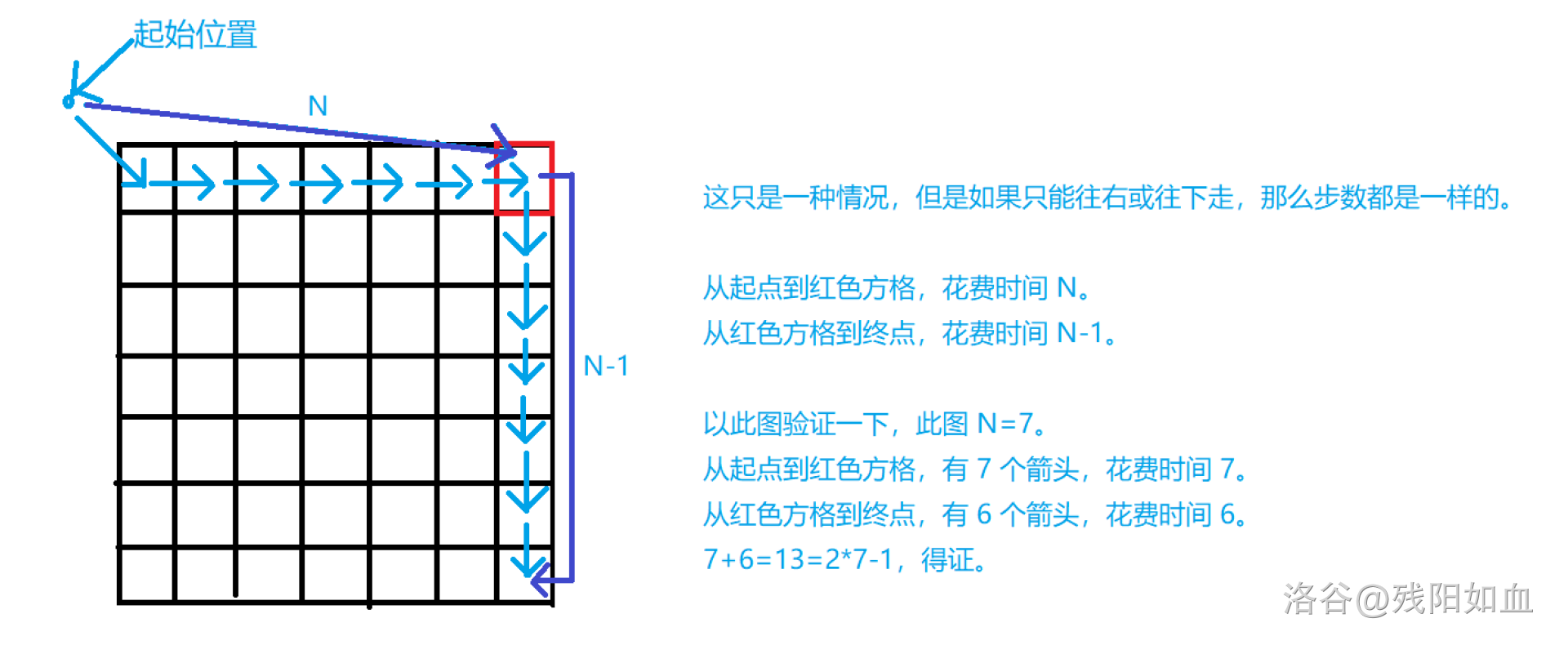
可以发现，如果我们只能向右或者向下走，那么花费的时间就恰好是 \(2N-1\)。当然，这条路径不走回头路，也就是最短路径，所以花费的时间 \(t\ge 2N-1\)。

从而我们可以得出一个重要的性质： 商人只能向右或者向下走。

这样，我们就使得状态的转移无后效性，DP 求解也就顺利成章了。

接下来分析同 摘花生 题解 类似，因而会比较简略一些。

状态表示

对于矩阵中的点 \((i,j)\)，定义状态 \(f_{i,j}\)。

集合

集合： 所有从 \((1,1)\) 到 \((i,j)\) 的所有路径。

属性

此处与 摘花生 不同！

这里要求 最小化 需要缴纳的费用，所有属性应为最小值，即 \(\min\)。

状态计算

因为只能向右或者向下，所以 \((i,j)\) 只能由 \((i-1,j)\) 和 \((i,j-1)\) 转移而来，所以可以将集合分为两部分：

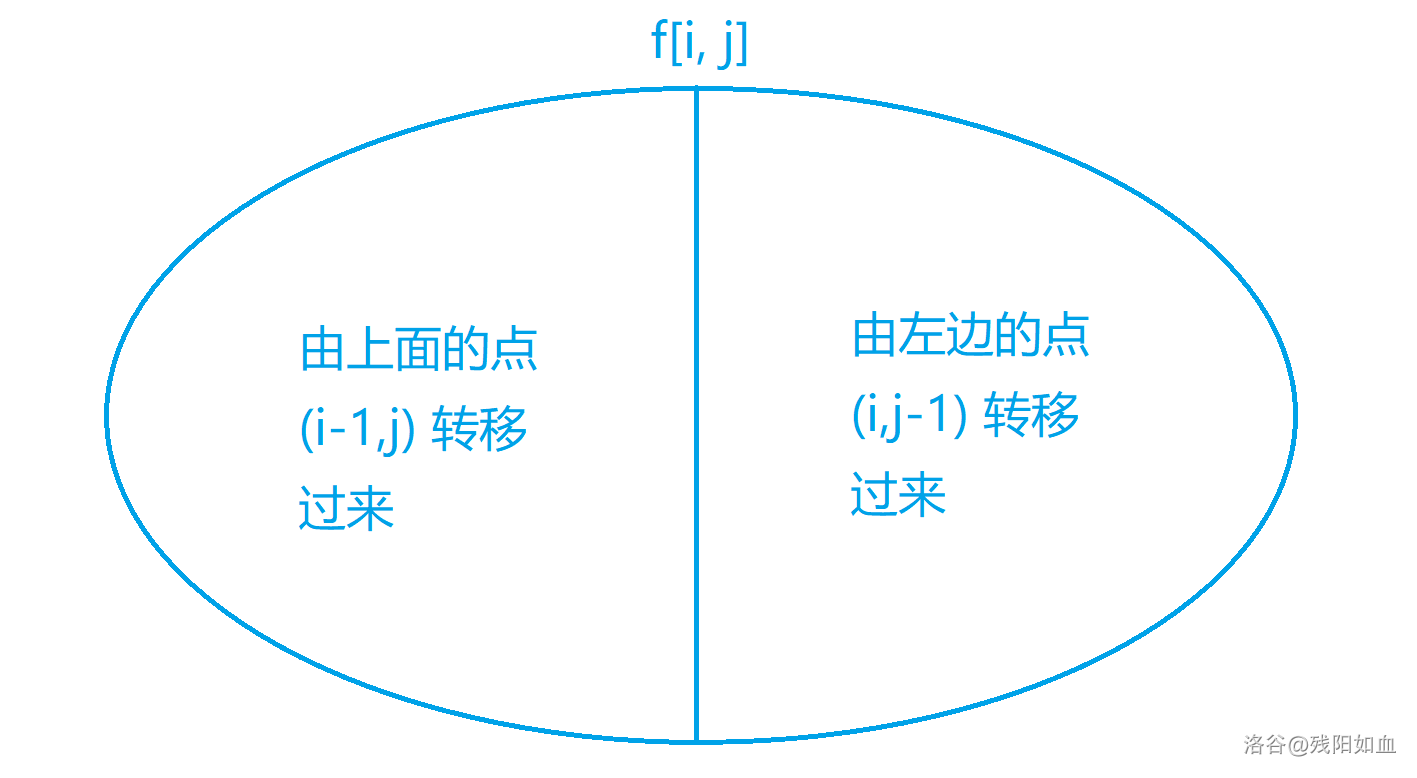
左边的集合如何计算？我们可以将其分为两步： \((1,1)\to(i-1,j)\to(i,j)\)。

其中，\((1,1)\to(i-1,j)\) 的描述是： 所有从 \((1,1)\) 到 \((i-1,j)\) 的所有路径，即 \(f_{i-1,j}\) 所表示的值。

接下来是 \((i-1,j)\to(i,j)\)。这一步中，取得的数值增大了 \(a_{i,j}\)，所以最终的结果中就要加上这一数值。

综上所述，左边的集合可以这样计算：\(f_{i-1,j}+a_{i,j}\)。

同理，右边的集合的计算方法：\(f_{i,j-1}+a_{i,j}\)。

由于属性是 \(\min\)，所以状态转移方程就是

\[f_{i,j}=\min\{f_{i-1,j}+a_{i,j},f_{i,j-1}+a_{i,j}\}=\min\{f_{i-1,j},f_{i,j-1}\}+a_{i,j}\]

接下来进行转移即可。

代码实现

实现细节

Q1：为什么要进行读入优化？

A1：因为读入的数字个数达到了 \((3\times 10^3)^2=9\times 10^6\)，读入量巨大，而未进行优化的 cin/cout 速度较慢，会导致程序超时。具体参见 常数优化技巧。

---

Q2：为什么 \(f\) 要先全部赋值为 0x3f3f3f3f，而 f[1][0]=f[0][1]=0？

A2：因为题目要求的最小值，为了方便 ~~懒得判断边界~~，使用 min 时对于网格外的位置需要赋值为 \(+\infty\)，而 C++ 中常用了替代 \(+\infty\) 的值为 0x3f3f3f3f。而 f[1][0]=f[0][1] 可以看成起点或者是更新起点的值，需要被取到且不影响最终结果，所以应该赋值为 \(0\)。

---

关于循环转移顺序的问题，参见 摘花生 题解。

最终代码

#include <cstring>
#include <iostream>
const int MAX = 3e3 + 10;

int N, f[MAX][MAX];

int main() {
  std::cin.tie(0)->sync_with_stdio(0); // 加速读入，当然也可以改用 scanf/printf
  std::cin >> N; memset(f, 0x3f, sizeof(f)); // 求 min，所以无关值需要赋值为正无穷。
  f[1][0] = f[0][1] = 0; // 起点需要特别处理
  for (int i = 1; i <= N; ++i)
    for (int j = 1; j <= N; ++j)
      std::cin >> f[i][j], f[i][j] += std::min(f[i - 1][j], f[i][j - 1]);
  std::cout << f[N][N] << std::endl;
  return 0;
}