「CSP2019 T」树上的数
背景
- Idea: CCF
- Data: CCF
- Solution: CCF
- 题面: CCF + oistream
描述
给定一个大小为 \(n\) 的树,它共有 \(n\) 个结点与 \(n-1\) 条边,结点从 \(1\sim n\) 编号。初始时每个结点上都有一个 \(1\sim n\) 的数字,且每个 \(1\sim n\) 的数字都只在 恰好 一个结点上出现。
接下来你需要进行 恰好 \(n-1\) 次删边操作,每次操作你需要选一条 未被删掉 的边,此时这条边所连接的两个结点上的数字将会 交换 ,然后这条边将被删去。
\(n-1\) 次操作过后,所有的边都将被删去。此时,按数字从小到大的顺序,将数字 \(1\sim n\) 所在的结点编号依次排列,就得到一个结点编号的排列 \(P_i\) 。现在请你求出,在最优操作方案下能得到的 字典序最小 的 \(P_i\)。
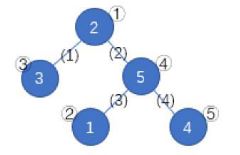
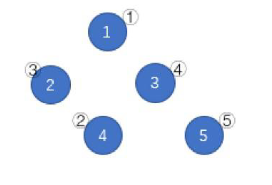
如上图,蓝圈中的数字 \(1\sim 5\) 一开始分别在结点 \(②,①, ③, ⑤, ④\)。按照 \((1)(4)(3)(2)\) 的顺序删去所有边,树变为下图。按数字顺序得到的结点编号排列为 \(①③④②⑤\),该排列是所有可能的结果中字典序最小的。
输入格式
本题输入包含多组测试数据。
第一行一个正整数 \(T\),表示数据组数。
对于每组测试数据:
第一行一个整数 \(n\),表示树的大小。
第二行 \(n\) 个整数,第 \(i~~(1\leq i\leq n)\) 个整数表示数字 \(i\) 初始时所在的结点编号。
接下来 \(n-1\) 行每行两个整数 \(x,y\) ,表示一条连接 \(x\) 号结点与 \(y\) 号结点的边。
输出格式
对于每组测试数据,输出一行共 \(n\) 个空格隔开的整数,表示最优操作方案下所能得到的字典序最小的 \(P_i\) 。
样例
样例输入1
4
5
2 1 3 5 4
1 3
1 4
2 4
4 5
5
3 4 2 1 5
1 2
2 3
3 4
4 5
5
1 2 5 3 4
1 2
1 3
1 4
1 5
10
1 2 3 4 5 7 8 9 10 6
1 2
1 3
1 4
1 5
5 6
6 7
7 8
8 9
9 10
样例输出1
1 3 4 2 5
1 3 5 2 4
2 3 1 4 5
2 3 4 5 6 1 7 8 9 10
数据规模与约定
对于所有测试点,\(1\leq T\leq 10\),保证给出的是一个数。其余性质如下表所示(若不填则同上一格)。
| 测试点编号 | \(n\leq\) | 特殊性质 |
|---|---|---|
| \(1\sim 2\) | \(10\) | 无 |
| \(3\sim 4\) | \(160\) | 树的形态是一条链 |
| \(5\sim 7\) | \(2000\) | |
| \(8\sim 9\) | \(160\) | 存在度数为 \(n-1\) 的结点 |
| \(10\sim 12\) | \(2000\) | |
| \(13\sim 16\) | \(160\) | 无 |
| \(17\sim 20\) | \(2000\) |
相关
在下列训练计划中: