描述

九条可怜是一个热爱出题的女孩子。

今天可怜想要出一道和图论相关的题。在一张无向图 \(G\) 上，我们可以对它进行一些非常有趣的变换，比如说对偶，又或者说取补。这样的操作往往可以赋予一些传统的问题新的活力。例如求补图的连通性、补图的最短路等等，都是非常有趣的问题。

最近可怜知道了一种新的变换：求原图的线图 (line graph)。对于无向图 \(G=\langle V,E \rangle\)，它的线图 \(L(G)\) 也是一个无向图：

(1). 它的点集大小为 \(|E|\)，每个点唯一对应着原图的一条边。

(2). 两个点之间有边当且仅当这两个点对应的边在原图上有公共点（注意不会有 自环 ）。

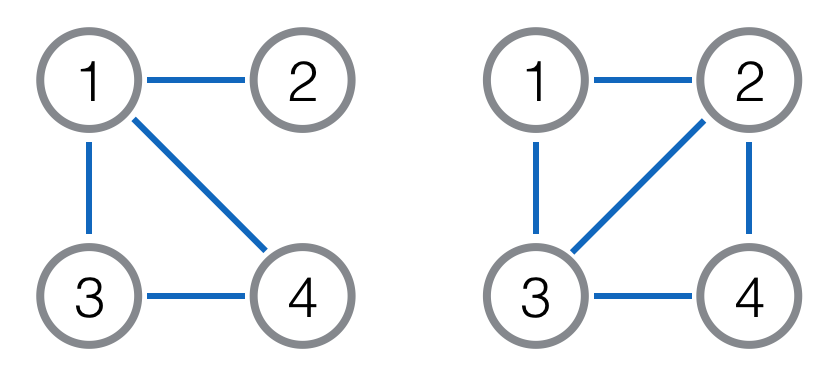
下图是一个简单的例子，左图是原图，右图是它对应的线图。其中点 \(1\) 对应原图的边 \((1,2)\)，点 \(2\) 对应 \((1,4)\)，点 \(3\) 对应 \((1,3)\)，点 \(4\) 对应 \((3,4)\)。

经过一些初步的摸索，可怜发现线图的性质要比补图复杂很多，其中突出的一点就是补图的补图会变回原图，而 \(L(L(G))\) 在绝大部分情况下不等于 \(G\)，甚至在大多数情况下它的点数和边数会以很快的速度增长。

因此，可怜想要从最简单的入手，即计算 \(L^k(G)\) 的点数（\(L^k(G)\) 表示对 \(G\) 求 \(k\) 次线图）。

然而遗憾的是，即使是这个问题，对可怜来说还是太困难了，因此她进行了一定的弱化。她给出了一棵 \(n\) 个节点的树 \(T\)，现在她想让你计算一下 \(L^k(T)\) 的点数。

格式

输入格式

第一行输入两个整数 \(n,k\)，表示树的点数以及连续求线图的次数。

接下来 \(n-1\) 行每行两个整数 \(u,v\) 表示树上的一条边。

输出格式

输出一行一个整数，表示答案对 \(998244353\) 取模后的值。

样例1

样例输入1

5 3
1 2
2 3
2 5
3 4

样例输出1

5

样例解释

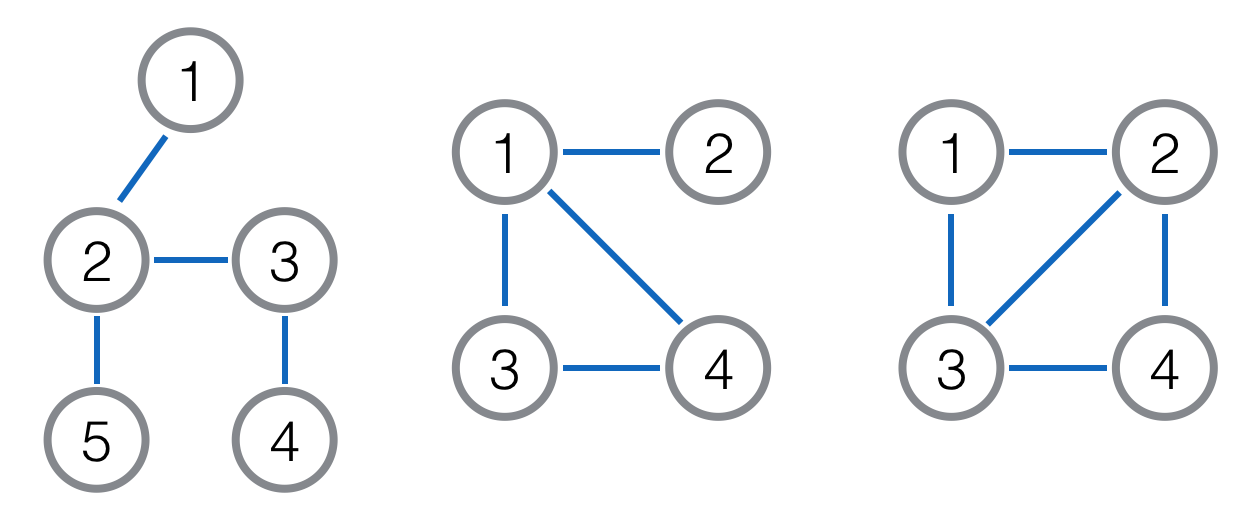
如下图所示，左图为原树，中图为 \(L(G)\)，右图为 \(L^2(G)\)。这儿并未画出 \(L^3(G)\)，但是由于 \(L^2(G)\) 有 \(5\) 条边，因此 \(L^3(G)\) 中有 \(5\) 个点。

限制

有 \(10\%\) 的数据，\(k=2\)。

有 \(10\%\) 的数据，\(k=3\)。

有 \(10\%\) 的数据，\(k=4\)。

有 \(20\%\) 的数据，\(k=5\)。

有 \(10\%\) 的数据，\(k=6\)。

有 \(10\%\) 的数据，\(k=7\)。

有 \(10\%\) 的数据，\(k=8\)。

有 \(20\%\) 的数据，\(k=9\)。

对于 \(100\%\) 的数据，\(2\le n\le 5000\)。

来源

ZJOI 2018 Round1