描述

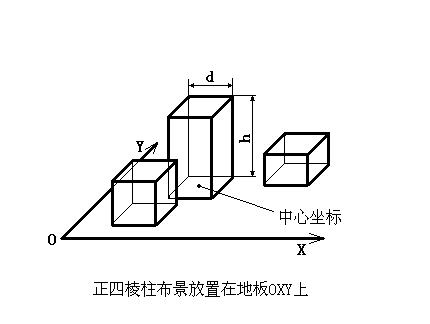
摄影师Tension在他的3D工作室里布置了一些布景（假设所有的布景都是正四棱柱，并且都直接放在地板上）。
为了描述这些布景的位置，我们在地板上建立了直角坐标系，原点O处是Tension和他的照相机。对于每一个正四棱柱的布景，用它的底面正方形的中心坐标(xc，yc)来标识它的位置，用底面边长d和棱柱的高h来标识它的形状（如图）。同时，每一布景的放置都是规则的，也就是说，所有棱柱底面的棱都平行于坐标轴。当然，任意两个布景（正四棱柱）是不可能有重叠的部分。

对于站在坐标原点O的Tension而言(Tension趴在地上，高度视为0)，一个四棱柱表面上的某个点，当且仅当它与原点的连线（也就是观察者的视线）不再穿过任何四棱柱的表面（包括棱和顶点）时，才被认为是可见的；如果一个四棱柱表面上存在可见的点，那么我们就认为这个四棱柱是可见的，这时，Tension就可以从照相机里看到这个布景（全部或者一部分）。
当Tensoin布置完这些布景之后，他想要了解从他所站的位置到底能够看到多少布景，但是当布景相当多的时候，这着实让Tension苦恼。而您的任务，就是利用程序求出在坐标原点O可见的四棱柱的个数m。

格式

输入格式

输入文件的第一行是一个正整数N，表示正四棱柱的总数。
从第2行至第N+1行，每行各有4个正整数xi，yi，di，hi，用空格分隔开，表示一个正四棱柱的中心坐标、底边长和高。

所有四棱柱的底面顶点坐标（x，y）都满足：
0＜x≤65000，0＜y≤65000；（也就是说，所有坐标都在第一象限内）
对于四棱柱的形状的限制有 0＜d≤65000，0＜h≤65000；
布景的总数为N，且1≤N≤1000。

输出格式

输出文件只有一个整数m，表示可见的正四棱柱的个数。

样例1

样例输入1

4
20 20 10 5
20 30  2 4
30 20  2 4
35 35 10 4

样例输出1

1

限制

每个测试点2s

来源

WinterCamp2001