0

gtz2009 LV 4 @ 2023-11-26 16:25:01

#include <bits/stdc++.h>
using namespace std;
const int MT = 1001;
const int MN = 101;
int T, n, f[MT], v[MN], w[MN];
int main()
{
    scanf("%d%d", &T, &n);
    for(int i = 1; i <= n; i++)
        scanf("%d%d", &w[i], &v[i]);
    for(int i = 1; i <= n; i++)
        for(int j = T; j >= w[i]; j--)
          f[j] = max(f[j], f[j - w[i]] + v[i]);
    printf("%d\n", f[T]);
    return 0;   
}

0

LucasRay LV 3 @ 2021-06-28 15:20:32

题目传送门

这是一道裸的01背包，不懂01背包的同学建议大家可以看一下教程

如果是已经学会的大佬请跳过

给定n种物品，每种物品都有重量wi和价值vi，每种物品只有一个。另外，背包容量为W。求解在不超过背包容量的情况下将哪些物品放入背包，才可以使背包中的物品价值之和最大。每种物品只有一个，要么不放入（0），要么放入（1），因此称之为01背包。
假设第i阶段表示处理第i种物品，第i-1阶段处理第i-1种物品，则当处理第i种物品时，前i-1中物品已经处理完毕，只需考虑第i-1阶段向第i阶段的转移。
状态表示：c[i][j]表示将前i种物品放入容量为j的背包中获得的最大价值。
第i种物品的处理状态包括以下两种
（1）不放入：放入背包的价值不增加，问题转化为“将前i-1种物品放入容量为j的背包中获得的最大价值”，最大价值为c[i-1][j]
（2）放入：在第i种物品放入之前为第i-1阶段，相当于从第i-1阶段向第i阶段转化。问题转化为“将前i-1种物品放入容量为j-w[i]的背包中获得的最大价值”，此时获得最大价值就是c[i-1][j-w[i]],再加上放入第i种物品获得的价值v[i]，总价值为c[i-1][j-w[i]]+v[i]
注意：若背包容量不足，则肯定不可以放入，所以仍为前i-1种的物品处理后的结果：若背包容量充足，则考察在放入、不放入哪种情况下获得的最大价值更大。

状态转移方程：
if (j < w[i])
c[i][j] = c[i-1][j];

else c[i][j] = max(c[i-1][j], c[i-1][j-w[i]]+v[i]);

算法步骤

1）初始化

c[0][j]=0,c[i][0]=0,其中i=0,1,2,…,n,j=0,1,2,…,W，表示第0种物品或背包容量为0时获得的价值为0；

2）循环阶段

(1) 按照状态转移方程处理第1种物品，得到c[1][j],j=1,2,…, W
(2)按照状态转移方程处理第2种物品，得到c[2][j], j=1,2,…, W.
(3)依次类推，得到c[n][j],j=1,2,…w.

3)构造最优解

c[n][W]就是不超过背包容量时可以放入物品的最大价值（最优值）。若还想知道具体放入了哪些物品，则根据c[][]数组逆向构造最优解。对此可以用一维数组x[]来存储解向量，x[i]=1表示第i种物品被放入背包，x[i]=0表示第i种物品未被放入背包。

(1)初始时i=n,j=W。

(2)若c[i][j]>c[i-1][j],则说明第i种物品被放入背包，令x[i]=1,j-=w[i];若c[i][j]<=c[i-1][j],则说明第i种物品没被放入背包，令x[i]=0。

(3)i--,转向第2步，直到 i=1时处理完毕。
此时已经得到解向量（x[1],x[2],…,x[n]），直接输出该解向量，也可以仅把x[i]=1的物品序号i输出。

算法代码：

推理过程请看图解：

回归正题，二维dp代码如下：
cpp //Lucas Ray #include <bits/stdc++.h> #define long long int using namespace std; const int maxn = 110; int t, m, ans = 0; int v[maxn], w[maxn], dp[maxn][maxn*10]; //v代表时间（即花费），w代表价值 int main() { scanf ("%d%d", &t, &m); for (int i = 1; i <= m; i++) { scanf ("%d%d", &v[i], &w[i]); } for (int i = 1; i <= m; i++) { for (int j = t; j >= 0; j--) { if (j >= v[i]) { dp[i][j] = max(dp[i-1][j-v[i]]+w[i], dp[i-1][j]); } else { dp[i][j] = dp[i-1][j]; } } } printf ("%d", dp[m][t]); return 0; }

二维dp AC记录

有的大佬看到这里就会说了：你这么菜啊，连一维优化都不会啊

算法优化！！！

状态表示：dp[j]表示将物品放入容量为j的背包中可以获得的最大价值。

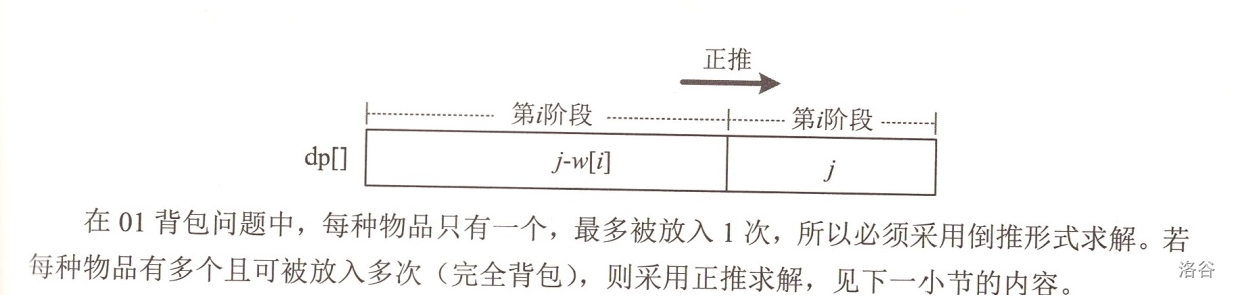
那就来看一维优化的代码吧

//Lucas Ray
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 3;
int dp[maxn];
int n, m;
int times[maxn], val[maxn];
inline int read() { //快读
    char a;
    int c=0,y=1;
    a=getchar();
    while(a<'0'||a>'9')
    {
        if(a=='-')
        {
            y=-1;
        }
        a=getchar();
    }
    while(a>='0'&&a<='9')
    {
        c=c*10+a-'0';
        a=getchar();
    }
    return c*y;
}
int main() {
    n = read(), m = read();
    for (int i = 1; i <= m; i++) {
        times[i] = read(), val[i] = read();
    }
    for (int i = 1; i <= m; i++) {
        for (int j = n; j >= 0; j--) {
            if (j >= times[i])
            dp[j] = max (dp[j], dp[j-times[i]] + val[i]);
        }
    }
    cout << dp[n] << endl;
    return 0;
}

这是蒟蒻发的第一篇题解，制作不易，不喜喷轻点

0

chenyiming LV 7 @ 2021-06-07 18:49:57

前面大佬的c++味儿太淡，看不懂（哭笑不得）
献上c++入门味儿

#include <bits/stdc++.h>
using namespace std;
int a[10001],b[10001];
int f[666666];
int main(){
    int w,n;
    cin>>w>>n;
    for (int i=1;i<=n;i++){
        cin>>a[i]>>b[i];
    }
    for (int i=1;i<=n;i++){
        for (int j=w;j>=a[i];j--){
            f[j]=max(f[j],f[j-a[i]]+b[i]);
        }
    }
    cout<<f[w];
    return 0;
}

0

伤风 LV 4 @ 2021-05-23 10:40:51

这是一道简单的01题，可以用二维来做，也可用一维；

#include<bits/stdc++.h>
using namespace std;
int f[1005][1005], w[1005], c[1005], n, m;
int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++)cin>>w[i]>>c[i];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            if(j<=w[i])
                f[i][j]=max(f[i][j],f[i-1][j-w[i]]+c[i]);
        }
    cout<<f[n][m]<<endl;
}

0

gsc LV 6 @ 2020-08-29 10:48:30

#include<bits/stdc++.h>
using namespace std;
int f[1001],w[1001],c[1001];
int main()
{
int m,n;
cin>>m>>n;
for(int i=1;i<=n;i++)
cin>>w[i]>>c[i];
for(int i=1;i<=n;i++)
for(int j=m;j>=w[i];j--)
{
if(f[j-w[i]]+c[i]>f[j])
f[j]=f[j-w[i]]+c[i];
}
cout<<f[m];
}

0

gsc LV 6 @ 2020-08-29 10:47:47

#include<bits/stdc++.h>
using namespace std;
int f[1001],w[1001],c[1001];
int main()
{
int m,n;
cin>>m>>n;
for(int i=1;i<=n;i++)
cin>>w[i]>>c[i];
for(int i=1;i<=n;i++)
for(int j=m;j>=w[i];j--)
{
if(f[j-w[i]]+c[i]>f[j])
f[j]=f[j-w[i]]+c[i];
}
cout<<f[m];
}

0

2132B LV 7 @ 2020-07-16 22:34:37

一道简单的动规题

01背包详情见OI WIKI

放code

#include<bits/stdc++.h>
using namespace std;
int v[10001],w[10001],f[10001],t,n;
int main()
{
    cin>>t>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>w[i]>>v[i];
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=t;j>=w[i];j--)
        {
            f[j]=max(f[j-w[i]]+v[i],f[j]);
        }
    }
    cout<<f[t];
    return 0;
}

0

j18tm01 LV 10 @ 2020-05-15 22:34:20

一维 dp 代码：


#include "stdio.h"
#include "iostream"
using namespace std;
int w[105], val[105];
int dp[1005];
int main()
{
    int t,m,res=-1;    
    scanf("%d%d",&t,&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&w[i],&val[i]);
    }
    for(int i=1;i<=m;i++) 
    {
        for(int j=t;j>=0;j--) 
        {
            if(j>=w[i])
            {
                dp[j]=max(dp[j-w[i]]+val[i], dp[j]);
            }
        }
    }    
    printf("%d",dp[t]);
    return 0;
}

0

Jong-oo LV 8 @ 2020-04-11 00:29:30

#include <iostream>             //[2005普及组-C]采药
#include <algorithm>
using namespace std;

int dp[1002];
int T, M, V[101], Ti[101];

int main()
{
    cin >> T >> M;
    for (int i = 1; i <= M; i++)
        cin >> Ti[i] >> V[i];

    for (int i = 1; i <= M; i++)
        for (int j = T; j >= Ti[i]; j--)
            dp[j] = max(dp[j], dp[j - Ti[i]] + V[i]);

    cout << dp[T] << endl;

    return 0;
}

0

雪虎 LV 7 @ 2018-11-04 11:07:11

Pascal代码
var
i,j,x,y,t,m:longint;
f:array[0..1000] of longint;
begin
readln(t,m);
for i:=1 to m do
begin
readln(x,y);
for j:=t downto x do
if f[j-x]+y>f[j] then f[j]:=f[j-x]+y;
end;
write(f[t]);
end.

0

SHZhang LV 8 @ 2018-08-11 15:29:12

#include <stdio.h>

/*背包问题：f[i][j]代表在前i个时间单位内，考虑前j株草药，所能得到的最大价值。*/

int f[1001][101];

int cost[101];
int value[101];

int t, m;

int max_val(int a, int b) {
    return a < b ? b : a;
}

int main()
{
    int i, j;
    scanf("%d%d", &t, &m);
    for (i = 1; i <= m; i++) {
        scanf("%d%d", cost + i, value + i);
    }
    for (i = 1; i <= t; i++) {
        for (j = 1; j <= m; j++) {
            f[i][j] = f[i][j-1];
            if (i >= cost[j]) {
                f[i][j] = max_val(f[i][j], f[i - cost[j]][j-1] + value[j]);
            }
        }
    }
    printf("%d", f[t][m]);
    return 0;
}

0

........ LV 7 @ 2017-11-06 16:30:30

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long t,m,a[1001],b[1001],f[100001];
int main()
{
cin>>t>>m;
for(int i=1;i<=m;i++)
cin>>a[i]>>b[i];
for(int i=1;i<=m;i++)
for(int j=t;j>=a[i];j--)
f[j]=max(f[j],f[j-a[i]]+b[i]);
cout<<f[t];
return 0;
}

0

Critical LV 6 @ 2017-11-06 13:12:34

这道题的数据范围比较弱，所以二维背包也可以跑过，理解二维背包主要是要理解第一和第二个中括号代表的东西，于是就很好解开了。
#include <bits/stdc++.h>
using namespace std;
int at,n;
int t[1005],m[1005];
int f[1005][1005];
int maxx(int x,int y){
if (x>y)return x;
else return y;
}
int main(){
scanf ("%d%d",&at,&n);
for (int i=1;i<=n;i++)scanf ("%d%d",&t[i],&m[i]);
for (int i=1;i<=at;i++)
for (int j=at;j>0;j--){
if (t[i]<=j)
f[i][j]=maxx(f[i-1][j],f[i-1][j-t[i]]+m[i]);//这里第一个代表选的药数；
else f[i][j]=f[i-1][j];//第二个代表剩余时间。
}
printf ("%d",f[n][at]);
return 0;
}

0

liuxinglin2660638656 LV 5 @ 2017-10-17 17:17:20

var
t,m,i,j,maxn:longint;
f:array[0..10000] of longint;
a,w:array[1..10000] of longint;
begin
readln(T,M);
for i:=1 to m do readln(a[i],w[i]);
f[0]:=0;
for i:=1 to m do
for j:=t downto 0 do
begin
if j>=a[i] then
f[j]:=max(f[j],f[j-a[i]]+w[i])
else f[j]:=f[j];
end;
maxn:=-maxlongint;
for j:=1 to t do
begin
if f[j]>maxn then maxn:=f[j];
end;
writeln(maxn);
end.

0

theWorld LV 6 @ 2017-09-27 22:36:01

一维
uses math;
var
t,m,i,j,maxn:longint;
f:array[0..10000] of longint;
a,w:array[1..10000] of longint;
begin
readln(T,M);
for i:=1 to m do readln(a[i],w[i]);
f[0]:=0;
for i:=1 to m do
for j:=t downto 0 do
begin
if j>=a[i] then
f[j]:=max(f[j],f[j-a[i]]+w[i])
else f[j]:=f[j];
end;
maxn:=-maxlongint;
for j:=1 to t do
begin
if f[j]>maxn then maxn:=f[j];
end;
writeln(maxn);
end.

0

theWorld LV 6 @ 2017-09-26 23:10:44

并不优美的二维
uses math;
var
t,m,i,j,maxn:longint;
f:array[0..1000,0..10000] of longint;
a,w:array[1..10000] of longint;
begin
readln(T,M);
for i:=1 to m do readln(a[i],w[i]);
f[0,0]:=0;
for i:=1 to m do
for j:=0 to t do
begin
if j>=a[i] then
f[i,j]:=max(f[i-1,j],f[i-1,j-a[i]]+w[i])
else f[i,j]:=f[i-1,j];

end;
maxn:=-maxlongint;
for j:=1 to t do
begin
if f[m,j]>maxn then maxn:=f[m,j];
end;
writeln(maxn);
end.

0

ccl66 LV 7 @ 2017-08-05 15:29:29

#include<cstdio>
#include<algorithm>
using namespace std;
int dp[1001],w[300],v[300];
int main()
{
    int t,m;
    scanf("%d%d",&t,&m);
    for(int i=1;i<=m;i++)
        scanf("%d%d",&w[i],&v[i]);
    for(int i=1;i<=m;i++)
        for(int j=t;j>=w[i];j--)
                dp[j]=max(dp[j-w[i]]+v[i],dp[j]);
    printf("%d\n",dp[t]);

    return 0;
}

0

PowderHan LV 10 @ 2017-05-08 07:56:27

/*
经典的0/1背包问题
对于每株药 我们都有采或者不采两种情况
直接0/1就好了
注意这里不要求时间全部用完
所以初始化为0就好了
够裸够粗暴
*/
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring> 
using namespace std;

const int MAXN=1005;
int T,n;
int f[MAXN];

int main()
{
    cin>>T>>n;
    int t,w;
    for(int i=1;i<=n;i++)
    {
        cin>>t>>w;
        for(int j=T;j>=t;j--)
            f[j]=max(f[j],f[j-t]+w);
    }
    cout<<f[T]<<endl;
    return 0;
}

0

coolxxx LV 9 @ 2016-08-15 16:34:47

测试数据 #0: Accepted, time = 0 ms, mem = 560 KiB, score = 10
测试数据 #1: Accepted, time = 0 ms, mem = 560 KiB, score = 10
测试数据 #2: Accepted, time = 0 ms, mem = 560 KiB, score = 10
测试数据 #3: Accepted, time = 0 ms, mem = 556 KiB, score = 10
测试数据 #4: Accepted, time = 0 ms, mem = 560 KiB, score = 10
测试数据 #5: Accepted, time = 0 ms, mem = 556 KiB, score = 10
测试数据 #6: Accepted, time = 0 ms, mem = 560 KiB, score = 10
测试数据 #7: Accepted, time = 0 ms, mem = 560 KiB, score = 10
测试数据 #8: Accepted, time = 0 ms, mem = 560 KiB, score = 10
测试数据 #9: Accepted, time = 0 ms, mem = 560 KiB, score = 10
Accepted, time = 0 ms, mem = 560 KiB, score = 100
题解+代码

0

咕咚国王 LV 4 @ 2016-08-14 14:55:12

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<algorithm>
using namespace std;
int f[2010],c[110],w[110]; //价值为[j]时背包的最大价值。每株草药的采摘时间。每株草药的价值。
int t,n; //总时间。总草药数。
int read() //读入优化，很好用，可以不写。
{
int p=1,x; char c;
while((c=getchar())<'0'||c>'9') if(c=='-')p=-1;
x=c-'0';
while((c=getchar())>='0'&&c<='9') x=x*10+c-'0';
return x*p;
}
int main() //标准01背包
{
t=read(); n=read();
for(int i=1;i<=n;i++)
c[i]=read(),w[i]=read();
//重点就是这个双重循环~~~
for(int i=1;i<=n;i++) //枚举草药
for(int j=t;j>=1;j--) //枚举价值，注意是倒序枚举，保证每株草药最多只被选一次。
if(j-c[i]>=0) //如果采摘当前株草药时间不能超过总时间。
f[j]=max(f[j],f[j-c[i]]+w[i]); //当前的最大价值由=max(不采当前草药能获得的最大价值，采当前草药能获得的最大价值)
cout<<f[t]; //好啦，最后一个肯定最大喽~
return 0;
}

题解

302 条题解

题目传送门

这是一道裸的01背包，不懂01背包的同学建议大家可以看一下教程

如果是已经学会的大佬请跳过

算法步骤

1）初始化

2）循环阶段

3)构造最优解

二维dp AC记录

有的大佬看到这里就会说了：你这么菜啊，连一维优化都不会啊

算法优化！！！

那就来看一维优化的代码吧

这是蒟蒻发的第一篇题解，制作不易，不喜喷轻点

一道简单的动规题

01背包详情见OI WIKI

采药

信息

状态

开发

支持

题解

302 条题解

题目传送门

这是一道裸的01背包，不懂01背包的同学建议大家可以看一下教程

~~如果是已经学会的大佬请跳过~~

算法步骤

1）初始化

2）循环阶段

3)构造最优解

二维dp AC记录

有的大佬看到这里就会说了：你这么菜啊，连一维优化都不会啊

算法优化！！！

那就来看一维优化的代码吧

这是蒟蒻发的第一篇题解，制作不易，不喜喷轻点

一道简单的动规题

01背包 详情见OI WIKI

采药

信息

状态

开发

支持

还没有账户？

登录

如果是已经学会的大佬请跳过

01背包详情见OI WIKI