建议在这个链接观看，渲染更佳：数字三角形 题解

题意简述

题目链接

Vijos ETO P1001（推荐）
Acwing 898
Luogu P1216

题目描述

给定一个的数字三角形，从**顶部**出发，在每一结点可以选择移动至其**左下方**的结点或移动至其**右下方**的结点，一直走到底层，要求找出一条路径，**使路径上的数字的和最大**。

输入输出样例

输入样例

5
7
3 8
8 1 0 
2 7 4 4
4 5 2 6 5

输出样例

30

样例解释

在上面的样例中，从 \(7→3→8→7→5\) 的路径产生了最大权值。

思路分析

贪心？

首先考虑是否可以贪心。

路径是不是需要经过**最大值**？
容易构造一组反例。

输入：

3
1
2 100
99 0 0

如果经过最大值 \(100\)，那么最终结果为 \(101\)；但是如果不这样走，通过路径 \(1\to2\to99\)，那么结果为 \(102\)，显然 \(102>101\)，所以这种贪心方法并不正确。

如果转而考虑次大值，次次大值，那么会在贪心的错误算法中越陷越深。此时，我们需要使用过其他的算法。

递归版动态规划（记忆化搜索）

爆搜

爆搜思路

既然贪心行不通，那么似乎没有什么好办法了，那么，我们可以考虑进行**搜索**，然后进行剪枝等优化。

爆搜代码

#include <iostream>
const int MAXN = 1e3 + 10;

int n, a[MAXN][MAXN];

int dfs(int x, int y) {
  if (x == n) return a[x][y]; // 边界条件
  return a[x][y] + std::max(dfs(x + 1, y), dfs(x + 1, y + 1));
  // 选择下一层的更大的计算出来的值加上当前值
}

int main() {
  std::cin >> n;
  for (int i = 1; i <= n; ++i)
    for (int j = 1; j <= i; ++j)
      std::cin >> a[i][j];
  std::cout << dfs(1, 1) << std::endl;
  return 0;
}

当然，上面的代码可以 等价变形 为如下代码：

#include <iostream>
const int MAXN = 1e3 + 10;

int n, a[MAXN][MAXN];

int dfs(int x, int y) {
  return a[x][y] + (x == n ? 0 : std::max(dfs(x + 1, y), dfs(x + 1, y + 1)));
  // 通过三目运算符简化代码
}

int main() {
  std::cin >> n;
  for (int i = 1; i <= n; ++i)
    for (int j = 1; j <= i; ++j)
      std::cin >> a[i][j];
  std::cout << dfs(1, 1) << std::endl;
  return 0;
}

爆搜时空复杂度分析

时间复杂度

对于每个递归到的点，都会扩展出两个需要递归的状态，所以时间复杂度是 \(\mathcal O(2^n)\) 的，非常低效。

空间复杂度（不严谨）

由于爆搜只记录了一条路径上的状态，而数字三角形的深度与 \(n\) 同级，所以空间复杂度为 \(\mathcal O(n)\)。

爆搜 \(\to\) 记搜

记搜思路

为什么爆搜这么 低效 ？容易发现，在爆搜的过程中，存在大量的重复计算。

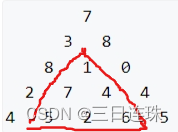
如样例中的三角形，分别递归到第二行的 \(3\) 与 \(8\) 时，分别递归计算了一次图中的红色三角形一次，产生了 重复计算 。同理，对于数字三角形中非最后一行的所有结点，都进行了多次重复计算，导致效率很低。

如何避免重复计算呢？考虑新增一个 \(f\) 数组，用 \(f_{x, y}\) 表示 dfs(x,y) 最终得到的结果。特别的，如果 \(f_{x, y}\) 为一个特殊值（自己命定）那么说明这个值还没有更新，需要进行计算；反之，这个值就已经计算过了，直接使用即可。

记搜代码

#include <cstring>
#include <iostream>
const int MAXN = 1e3 + 10;
const int INF = 0x3f3f3f3f;
// INF 为特殊值，且不会在最终结果中出现，容易用 memset 赋值

int n, a[MAXN][MAXN], f[MAXN][MAXN];

int dfs(int x, int y) {
  if (f[x][y] != INF) return f[x][y];
  // 如果已经计算过，直接返回
  return f[x][y] = a[x][y] + std::max(dfs(x + 1, y), dfs(x + 1, y + 1));
  // 进行计算，利用了 C++ 赋值表达式有返回值的特性
}

int main() {
  memset(f, 0x3f, sizeof(f)); // 赋值为 INF
  std::cin >> n;
  for (int i = 1; i <= n; ++i)
    for (int j = 1; j <= i; ++j)
      std::cin >> a[i][j];
  std::cout << dfs(1, 1) << std::endl;
  return 0;
}

记搜时空复杂度分析

时间复杂度

由于每个结点 只会被计算一次 ，所以时间复杂度与结点数量同级，为 \(\mathcal O(n^2)\)。

空间复杂度（不严谨）

同爆搜，空间复杂度为 \(\mathcal O(n)\)。

循环版动态规划

递归 \(\to\) 循环

递归由于需要调用栈，所以通常效率略低于循环（但是一般不差这一点时间）。由于记搜需要向下许多层，所以考虑从下往上，从左往右依次 dfs 每个结点，这样 dfs 的栈就限制在了一层，加快了时间。

由于 dfs 只限制在了一层，所以我们可以发现 dfs 的外壳可以根本不需要，直接循环遍历即可。

循环动归思路（简略）

定义数组 \(f_{x, y}\) 表示从最后一行走到 \((x, y)\) 经过的所有路径的最大值。

其中 \((x, y)\) 的两个转移路径分别是从 \((x+1,y)\) 和 \((x+1,y+1)\) 进行转移，所以容易得出动态规划转移方程 \(f_{x,y}=\max\{f_{x+1,y}+w_{x,y},f_{x+1,y+1}+w_{x,y}\}=\max\{f_{x+1,y},f_{x+1,y+1}\}+w_{x,y}\)。其中 \(w_{x,y}\) 表示 \((x,y)\) 上的数值。

循环动归代码

#include <iostream>
const int MAXN = 1e3 + 10;

int n, a[MAXN][MAXN], f[MAXN][MAXN];
// a 为读入的数字三角形, f 为状态数组

int main() {
  std::cin >> n;
  for (int i = 1; i <= n; ++i)
    for (int j = 1; j <= i; ++j) std::cin >> a[i][j], f[i][j] = a[i][j];
  // f[i][j] = a[i][j] 是为了方便避免将 f[n][1~n] 重新赋值为 a[n][1~n]，直接写可以节省码量
  for (int i = n - 1; i; --i) // 从最后一行往上遍历
    for (int j = 1; j <= i; ++j)
      f[i][j] += std::max(f[i + 1][j], f[i + 1][j + 1]); // 根据状态转移方程转移
  std::cout << f[1][1] << std::endl;
  // f[1][1] 表示从最后一行走到 (1,1) 的所有路径的最大值，写就是最后所求
  return 0;
}

循环动归时空复杂度分析

时间复杂度

显然，该代码时间复杂度为 \(\mathcal O(n^2)\)。

空间复杂度

由于定义了两个 \(n\times n\) 的数组，所以空间复杂度为 \(\mathcal O(n^2)\)。

空间优化

观察代码发现，a 数组读入后就没有再次使用过，且读入后立即 f[i][j]=a[i][j]，所以发现 a 数组并没有存在的必要，可以直接省略掉。

#include <iostream>
const int MAXN = 1e3 + 10;

int n, f[MAXN][MAXN];

int main() {
  std::cin >> n;
  for (int i = 1; i <= n; ++i)
    for (int j = 1; j <= i; ++j) std::cin >> f[i][j]; // 直接用 f 代替 a
  for (int i = n - 1; i; --i)
    for (int j = 1; j <= i; ++j)
      f[i][j] += std::max(f[i + 1][j], f[i + 1][j + 1]);
  std::cout << f[1][1] << std::endl;
  return 0;
}