背景

• Idea: CCF
• Data: CCF
• Solution: CCF
• 题面: CCF + LOJ@EntropyIncreaser + oistream（上传）

描述

黑板上写有 \(n\) 个互不相等且都小于 \(p\) 的正整数 \(a_1,a_2,\cdots ,a_n\)。小 J 想用这些数字和小 M 玩一个猜数游戏。

游戏规则十分简单：游戏开始时，小 J 会从这些数字中随机选择若干个让小 M 来猜，而小 M 则可以通过若干次 询问 来确定小 J 选择了哪些数字。

每一次 询问 的模式如下：小 M 可以任意指定一个数字 \(a_k\)，若它是小 J 所选择的数字之一，则小 J 会告诉小 M 他所选择的数字中所有能表示成 \({a_k}^m\mod p\)的数，其中 \(m\) 是任意正整数，\(\operatorname{mod}\) 表示求二者做带余除法后的余数。反之，若 \(a_k\) 没有被小 J 选中，则小 J 只会告诉小 M \(a_k\) 没有被选中。

游戏会在小 M 确定小 J 所选中的所有数字后立刻结束。

例如，若 \(n=4\)，\(p=7\) ，数字 \(\{a_n\}\) 按下标顺序依次为 \(\{1,3,4,6\}\)，小 J 选定的数字为 \(\{1,4,6\}\)，一种可能的游戏进行的过程（并非是最优过程）如下：

小 M 的询问	小 J 的反馈
\(a_2=3\)	\(a_2\) 没有被选中
\(a_4=6\)	\(6(=6^1\mod 7),1(=4^3\mod 7)\)
\(a_3=4\)	\(4(4^1\mod 7),1(=4^3\mod 7)\)

\(3\) 次询问后小 J 所选出的所有数都已被小 M 确定，游戏结束。

小 M 还有作业没有写完，因此他需要对游戏进行的时间进行评估。他想知道为了使游戏结束，他所需要做出询问的最小次数的期望 \(S\) 是多少。

为了避免精度误差，你需要输出答案乘 \(2^n-1\) 后模 \(998244353\) 的余数。在本题中，你可以认为小 J 每次在选数时会在集合 \(\{a_1,a_2,\cdots ,a_n\}\)的全部 非空子集 中等概率地选择一个，在这个前提下可以证明 \((2^n-1)\times S\)一定是一个整数。

输入格式

第一行两个正整数 \(n\) 和 \(p\)。

第二行 \(n\) 个正整数，依次表示 \(a_1,a_2,\times ,a_n\)。

输出格式

仅一行一个整数表示答案。

样例

输入样例1

4 7
1 3 4 6

输出样例1

17

样例输入2

8 9
1 2 3 4 5 6 7 8

样例输出2

532

样例解释

样例解释1

下表给出了小 J 所选的子集与小 M 最小询问次数的关系。

小 J 所选的子集	最优的询问集合
\(\{1\}\)	\(\{1\}\)
\(\{3\},\{3,4\},\{3,6\},\{3,4,6\},\{1,3\},\{1,3,4\},\{1,3,6\},\{1,3,4,6\}\)	{3}
\(\{4\},\{1,4\}\)	\(\{4\}\)
\(\{6\},\{1,6\}\)	\(\{6\}\)
\(\{4,6\},\{1,4,6\}\)	\(\{4,6\}\)

因此最小询问次数的期望 \(S=\dfrac{17}{15}\)。

数据规模与约定

对于所有测试点： \(1\leq n\leq 5000\)，\(3\leq p\leq 10^8\)，\(1\leq a_i\leq p~~(1\leq i\leq n)\) 且 \(a_i\) 两两不同。

对于所有编号为奇数的测试点，保证 \(p\) 是一个素数；对于所有编号为偶数的测试点，保证存在奇素数 \(q\) 和正整数 \(k>1\) 使得 \(p=q^k\)。

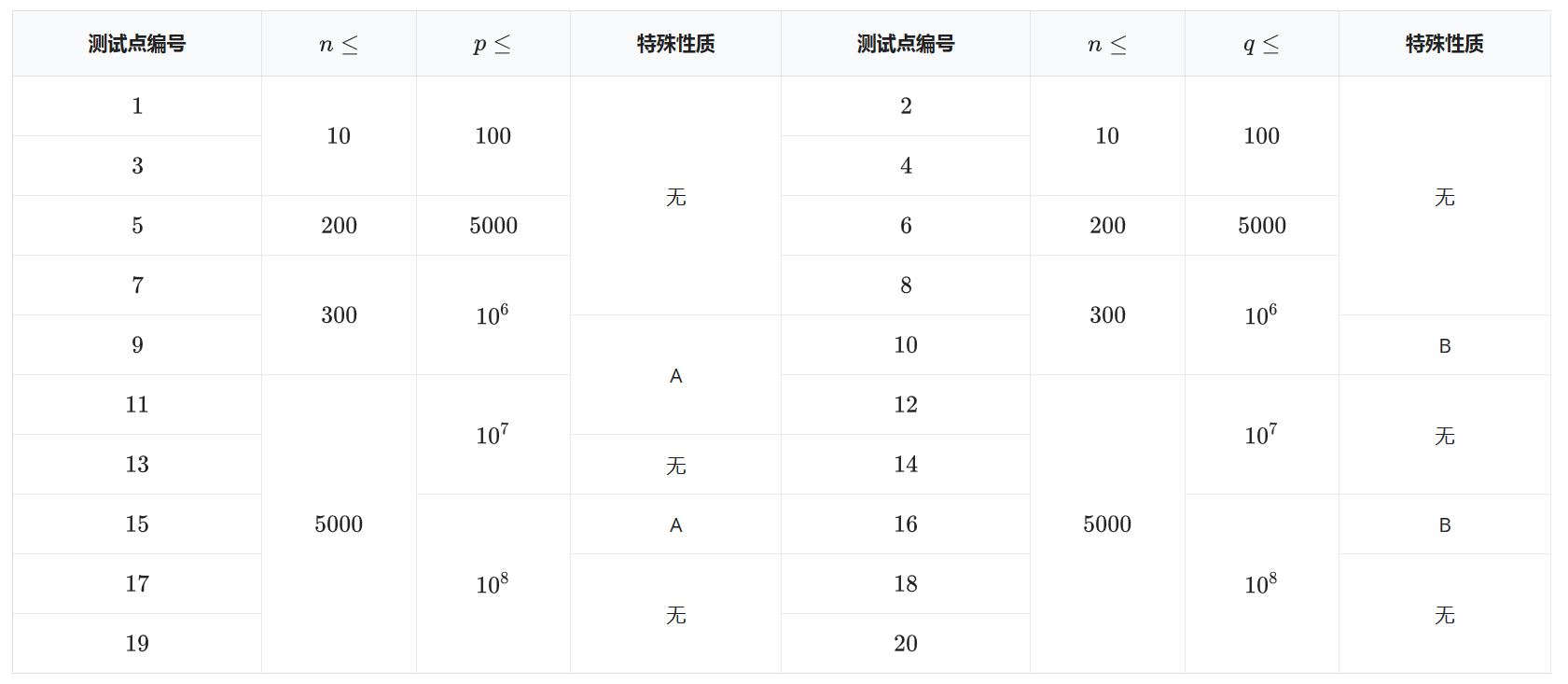
（上传者注：此图源自 LibreOJ）

特殊性质 A：在模 \(p\) 意义下 \(3^i~~(1\leq i\leq p-1)\) 两两不同余。

特殊性质 B：对所有的 \(1\leq i\leq n\) 都有 \((a_i,p)>1\) 。