防护伞

我们可以看出，只要我们计算出了这个圆形伞面的 \(r\)，或者 \(r^2\)，就可以求出圆形伞面的面积。那么我们如何去求呢？

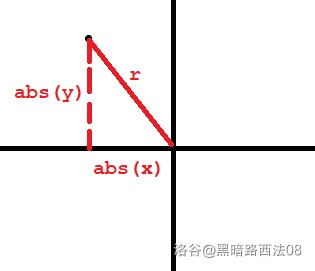
如上图，据勾股定理可得 \(r=\sqrt{(abs(x)^2+abs(y)^2)}\)，即\(r=\sqrt{(x^2+y^2)}\)，但我们没必要求出具体的 \(r\)，因为我们求出 \(r^2\) 即可。所以，伞面面积为 最大的\((x×x+y×y)×3.1415926535\)。

#include<bits/stdc++.h>
#define pi 3.1415926535 
using namespace std;
int n,r2=INT_MIN;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        int x,y;
        cin>>x>>y;
        r2=max(r2,x*x+y*y);//如同解释一样，求出最大的 r^2
    }
    printf("%.4lf\n",pi*r2);//圆面积，注意精确后 4 位 
    return 0;
}