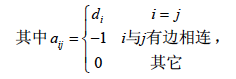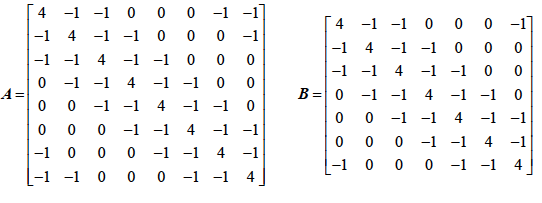描述

最近，小栋在无向连通图的生成树个数计算方面有了惊人的进展，他发现：
n 个结点的环的生成树个数为n。
n 个结点的完全图的生成树个数为nn-2。
这两个发现让小栋欣喜若狂，由此更加坚定了他继续计算生成树个数的想法，他要计算出各种各样图的生成树数目。
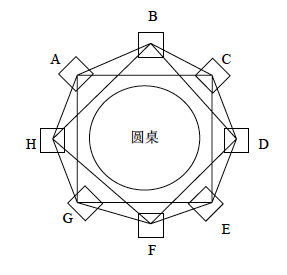
一天，小栋和同学聚会，大家围坐在一张大圆桌周围。小栋看了看，马上想到了生成树问题。如果把每个同学看成一个结点，邻座（结点间距离为1）的同
学间连一条边，就变成了一个环。可是，小栋对环的计数已经十分娴熟且不再感兴趣。于是，小栋又把图变了一下：不仅把邻座的同学之间连一条边，还把相隔一个座位（结点间距离为2）的同学之间也连一条边，将结点间有边直接相连的这两种情况统称为有边相连，如图1 所示。

图1
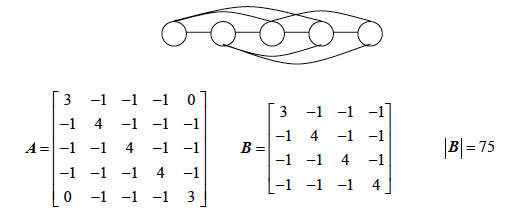
小栋以前没有计算过这类图的生成树个数，但是，他想起了老师讲过的计算任意图的生成树个数的一种通用方法：构造一个n×n 的矩阵A={aij}

其中di 表示结点i 的度数。
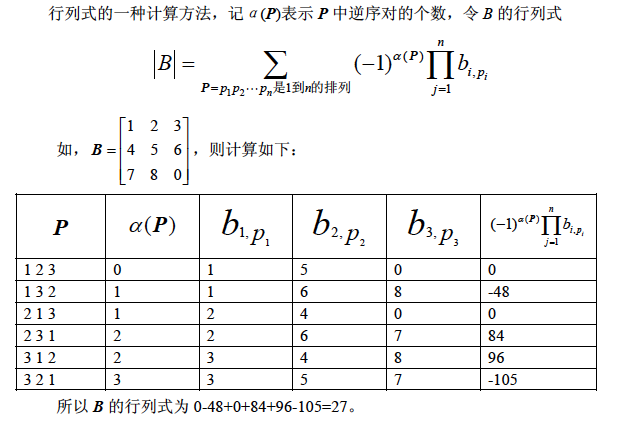
与图1 相应的A 矩阵如下所示。为了计算图1 所对应的生成数的个数，只要去掉矩阵A 的最后一行和最后一列，得到一个(n-1)×(n-1)的矩阵B，计算出矩阵B 的行列式的值便可得到图1 的生成树的个数。

所以生成树的个数为B = 3528。小栋发现利用通用方法，因计算过于复杂而很难算出来，而且用其他方法也难以找到更简便的公式进行计算。于是，他将图做了简化，从一个地方将圆桌断开，这样所有的同学形成了一条链，连接距离为1 和距离为2 的点。例如八个点的情形如下：

这样生成树的总数就减少了很多。小栋不停的思考，一直到聚会结束，终于
找到了一种快捷的方法计算出这个图的生成树个数。可是，如果把距离为3 的点也连起来，小栋就不知道如何快捷计算了。现在，请你帮助小栋计算这类图的生成树的数目。

格式

输入格式

输入中包含两个整数k, n(k≤5，n≤10^15)，由一个空格分隔。k 表示要将所有距离不超过k（含k）的结点连接起来，n 表示有n 个结点。

输出格式

输出一个整数，表示生成树的个数。由于答案可能比较大，所以你只要输出答案除65521 的余数即可。

样例1

样例输入1

3 5

样例输出1

75

限制

每个测试点1s。

提示

样例说明：
样例对应的图如下：

来源

NOI 2007 Day 2