测试数据来自 system/1126

题目描述

在平面上有 \(n\) 个点，每个点用一对整数坐标表示。例如：当 \(n=4\) 时，\(4\) 个点的坐标分别为：\(p_1(1,1)\)，\(p_2(2,2)\)，\(p_3(3,6)\)，\(p_4(0,7)\)，见图一。

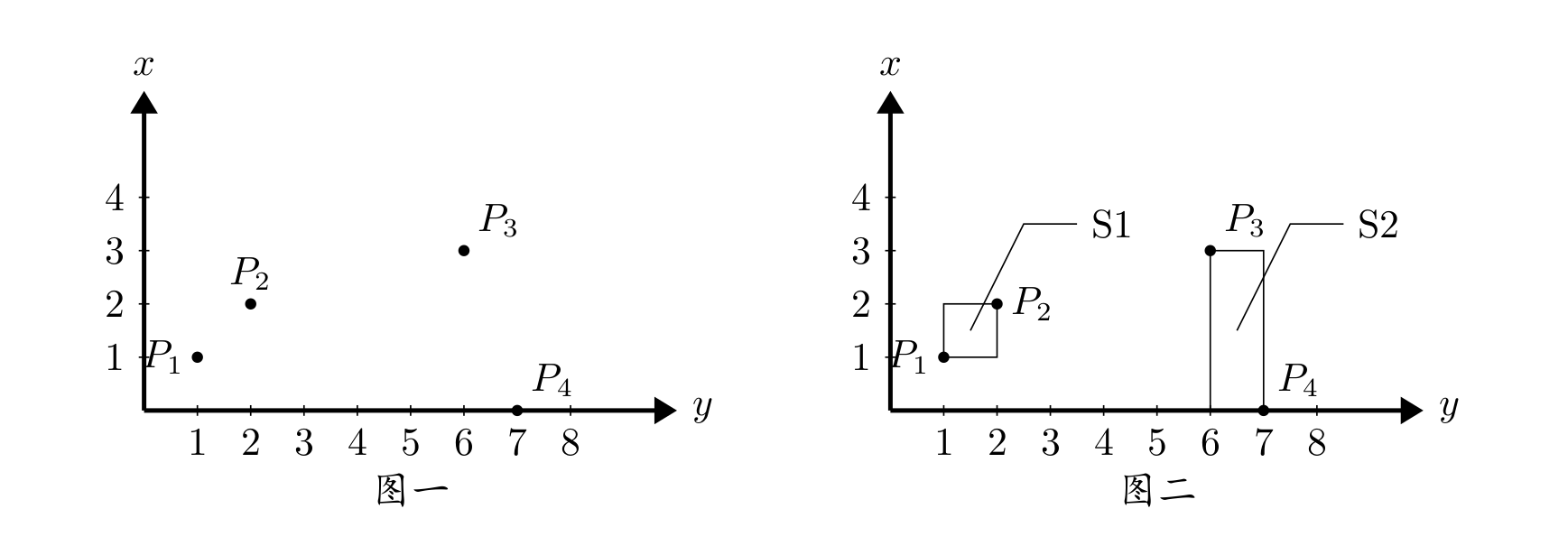
这些点可以用 \(k\) 个矩形全部覆盖，矩形的边平行于坐标轴。当 \(k=2\) 时，可用如图二的两个矩形 \(s_1,s_2\) 覆盖，\(s_1,s_2\) 面积和为 \(4\)。问题是当 \(n\) 个点坐标和 \(k\) 给出后，怎样才能使得覆盖所有点的 \(k\) 个矩形的面积之和为最小呢？

约定：覆盖一个点的矩形面积为 \(0\)；覆盖平行于坐标轴直线上点的矩形面积也为 \(0\)。各个矩形必须完全分开（边线与顶点也都不能重合）。

输入格式

第一行共两个整数 \(n,k\)，含义如题面所示。

接下来 \(n\) 行，其中第 \(i+1\) 行有两个整数 \(x_i,y_i\)，表示平面上第 \(i\) 个点的坐标。

输出格式

共一行一个整数，为满足条件的最小的矩形面积之和。

输入输出样例 #1

输入 #1

4 2
1 1
2 2
3 6
0 7

输出 #1

4

说明/提示

对于 \(100\%\) 数据，满足 \(1\le n \le 50\)，\(1 \le k \le 4\)，\(0 \le x_i,y_i \le 500\)。

【题目来源】

NOIP 2002 提高组第四题