测试数据来自 system/1683

背景

经典题

描述

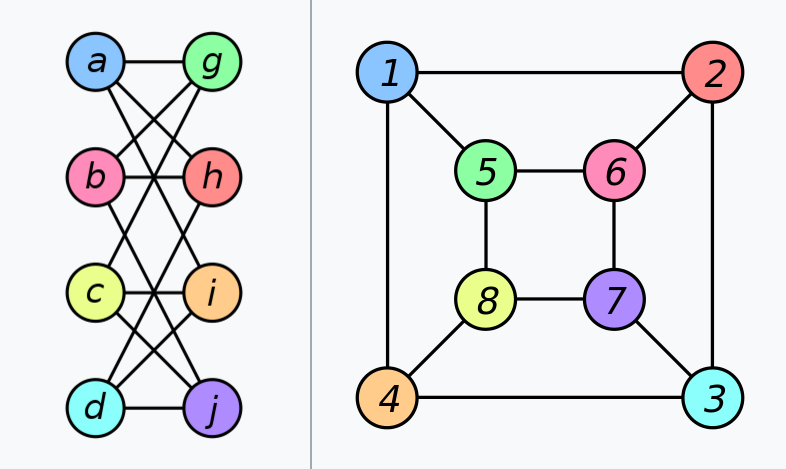
所谓图的同构是指两个图“相同”。图的同构有着广泛的应用，比如当要对一批图施行某种操作的时候，如果能发现其中有一些图是同构的，就可以在这些同构的图中只保留一个，从而降低工作量。例如，图1所示的T1和T3就是同构的。

图的同构的定义：给出两个图G1=（V1，E1），G2=（V2，E2）。如果存在一个V1到V2的一一映射f，使得（x，y）是G1的边，当且仅当（f（x），f（y））是G2的边，则称G1和G2是同构的。也就是说，我们只关心顶点间的拓扑关系而不关心顶点的编号。
任意图的同构的判定尚无有效的算法，但要判断两棵树是否同构则要容易些。下面我们仅考虑有根树（即树形图：有向图，存在一个根，入度为0，从根到其他任一顶点恰好有一条有向路）。给出k棵有根树T1，T2，…，Tk，每棵树都有n个顶点，你的任务是求出这些树在同构关系下的所有等价类（如果两棵树同构，则它们属于同一个等价类）。

格式

输入格式

输入的第1行包含两个整数k（1<=k<=100）和n（1<=n<=50），表示总共有k棵树，每棵都是n个顶点。接下来k行，每行描述一棵树；每行包含n-1对整数，表示这棵树的n-1条有向边；数字间用空格隔开。顶点的编号为1到n，每对整数xy表示存在一条x指向y的有向边。树的编号和在数据中出现的顺序一致，也就是说输入文件中第2行描述的是T1，第3行描述的是T2，……，第k+1行描述的是Tk。

输出格式

把给出的k棵树划分为不同的等价类，使得同一等价类中任意两棵树同构。对于每个等价类，从小到大输出这个等价类中的树的编号，用等号隔开。如果有m个等价类，则按字典序输出，每个一行。例如，有4个等价类{4，2，7}，{5，1，3}，{8，9}，{6}，则输出
1=3=5
2=4=7
6
8=9
注意，数字和等号之间不要有空格；行首和行末可以有空格。

样例1

样例输入1

3 7
7 2 7 1 7 6 2 3 1 4 6 5
7 2 7 1 2 3 1 4 1 5 5 6
4 3 3 2 4 1 1 7 5 6 4 5

样例输出1

1=3
2

限制

1s