「BJSS2020 J」装备升级【无数据】
暂无测试数据。
背景
- Idea: 北京市赛
- Data: 暂无
- Std: 北京市赛
- 题面: 北京市赛+oistream
描述
忆艾现在手头有 \(n\) 件装备,这些装备目前都是初始状态,我们称之为 \(0\) 级,每件装备恰好可以升级两次,第 \(i\) 件装备从 \(0\) 级升级到 \(1\) 级需要 \(w_{i,1}\) 枚金币,从第 \(1\) 级升级到第 \(2\) 级需要 \(w_{i,2}\) 枚金币。
忆艾想知道如果她总共给装备升级次数为 \(m\),至少需要花费多少枚金币。
输入格式
- 第一行两个正整数 \(n,m\) 表示总共的装备数量和需要升级的次数。
- 接下来共 \(n\) 行,每行两个正整数 \(w_{i,1},w_{i,2}\) 表示第 \(i\) 件装备两次升级分别需要花费的金币。
输出格式
输出一行一个正整数,表示最少需要花费多少枚金币。
样例
输入样例1
5 7
1 3
2 1
2 5
4 2
1 1
输出样例1
11
样例解释1
选择升级的装备分别是:
- 第一件装备升 \(2\) 级。
- 第二件装备升 \(2\) 级。
- 第三件装备升 \(1\) 级。
- 第五件装备升 \(2\) 级。
总共花费的金币是 \((1+3)+(2+1)+2+(1+1)=11\) 枚。
输入样例2
见附加文件。
输出样例2
见附加文件。
数据规模与约定
对于 \(100\%\) 的数据,保证 \(1\leq n\leq 5\times 10^5,1\leq m\leq 2\times n,w_{i,j}\leq 10^9\)。
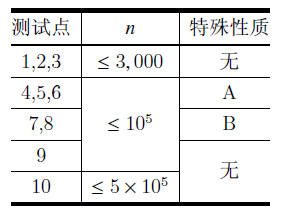
- 特殊性质 \(\text{A}\):对所有 \(i\),满足 \(w_{i,1}\geq w_{i,2}\)。
- 特殊性质 \(\text{B}\):对所有 \(i\),满足 \(w_{i,1}\leq w_{i,2}\)。