有向图的强连通分量
有向图的强连通分量
基本概念
在无向图中,若从顶点 \(u\) 到顶点 \(v\) 有路径,则称顶点 \(u\) 与 \(v\) 是连通的;
如果图中任意一对顶点都是连通的,则称此无向图是连通图。
对于一个无向非连通图,可以通过深度优先搜索或广度优先搜索来获取它的连通分量:从一个未访问过的节点开始进行深度优先或者广度优先搜索,其能到达的所有顶点及其相关的边构成的子图就是一个连通分量;直到访问完全部的节点,便可以获取该图的所有连通分量。
有向图强连通分量:在有向图 \(G\)中,如果两个顶点 \(u,v\) 间有一条从 \(u\) 到 \(v\) 的有向路径,同时还有一条从 \(v\) 到 \(u\) 的有向路径,则称两个顶点强连通。如果有向图 \(G\) 的每两个顶点都强连通,称 \(G\) 是一个 强连通图。有向图的极大强连通子图,称为 强连通分量。
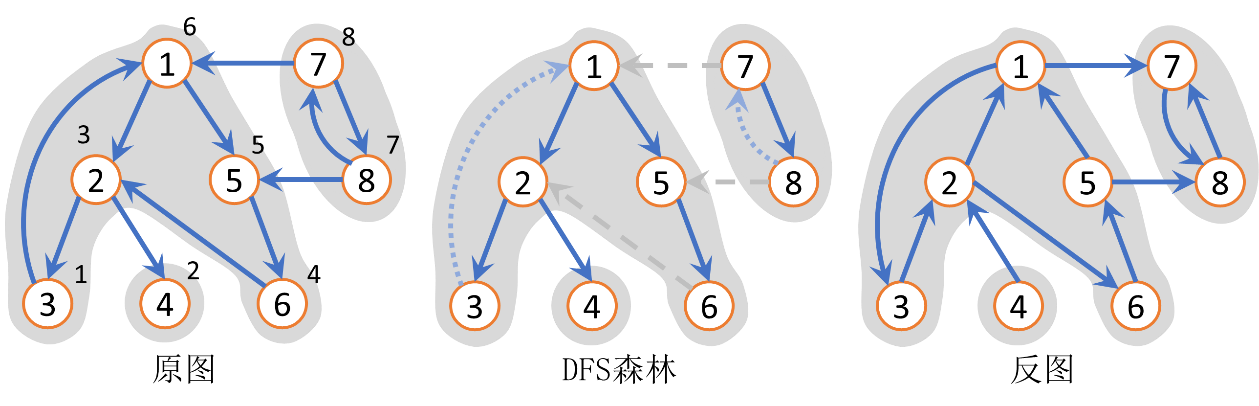
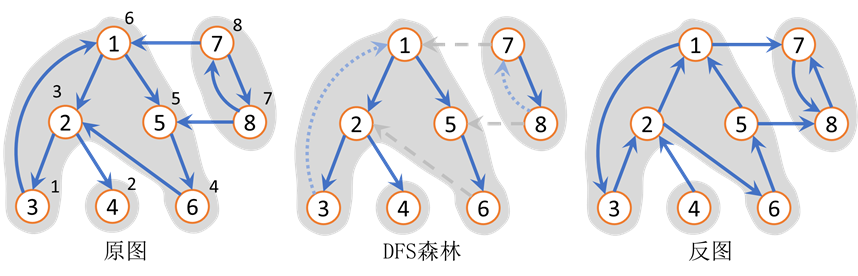
利用深度优先搜索算法,从图 \(G\) 的任一结点开始,沿着结点的出弧(边)遍历,当无法再遍历时,得到一颗 深搜树 (\(\texttt{DFS}\) 树),再选择 \(G\) 中任意一个未访问过的结点继续遍历,直到访问完所有结点,所产生的多棵树称之为 深搜森林 ;
离开时间戳:\(\texttt{DFS}\) 生成森林时,访问完某个结点 \(u\) 及 \(u\) 的所有子结点准备回溯时,记录的计数值。既是第几个访问结束的结点。性质:子树的根的时间戳总是子树上所有结点中最大的。
一个有向图的弧,我们把它分成三类: 树枝弧、回弧、横叉弧。
树枝弧:\(\texttt{DFS}\) 生成树上的弧;
回弧:不在 \(\texttt{DFS}\) 生成树中,由 \(\texttt{DFS}\) 树中结点回指向直系祖先结点的弧;
横叉弧:不在DFS生成树中,由 \(\texttt{DFS}\) 树中结点指向亲戚结点(除直系祖先)的弧;
\(\texttt{Kosaraju}\) 算法原理
问题一、对有向图 \(G\) 做 \(\texttt{DFS}\) 获得森林, 先遍历到的结点会有横叉弧指向后遍历到的结点吗?反之,后遍历到的结点会有横叉弧指向先遍历到的结点吗?
第一问不会。先遍历得到的结点 \(u\) 如果存在横叉弧指向后遍历到的结点 \(v\),那么在遍历 \(u\) 时就会将横叉弧作为树枝弧遍历到 \(v\) 结点。第二问则可能会有。
问题二、对有向图做 \(\texttt{DFS}\) 获得森林,如果这个森林有多棵树,那么 任一个强连通分量会存在于多颗树中吗? 为什么?
不会。强连通分量中的任意两个节点都必须有往返路径。那么在遍历到分量中任一结点后,就能遍历到分量中的所有结点。
问题三、一棵树(或子树的)的根,可以保证到其子结点,在原图中都是有路径可达的。 那么如何找到哪些结点到该根也是有路径的呢?
以该根在反图中 \(\texttt{DFS}\),能够遍历到的点说明有路径可达该根。
问题四、如何查找包含 \(u\) 点的强连通分量中的所有结点?
由问题三可知,以结点 \(u\) 为根在原图中做 \(\texttt{DFS}\),再以 \(u\) 为根在反图中做 \(\texttt{DFS}\),获得两棵树,两棵树中都有的结点,既可以保证 \(u\) 到这些结点有路径,也可以保证这些结点到 \(u\) 有路径。 那么可以保证这些结点互相之间都有来回路径,这就是强连通分量。
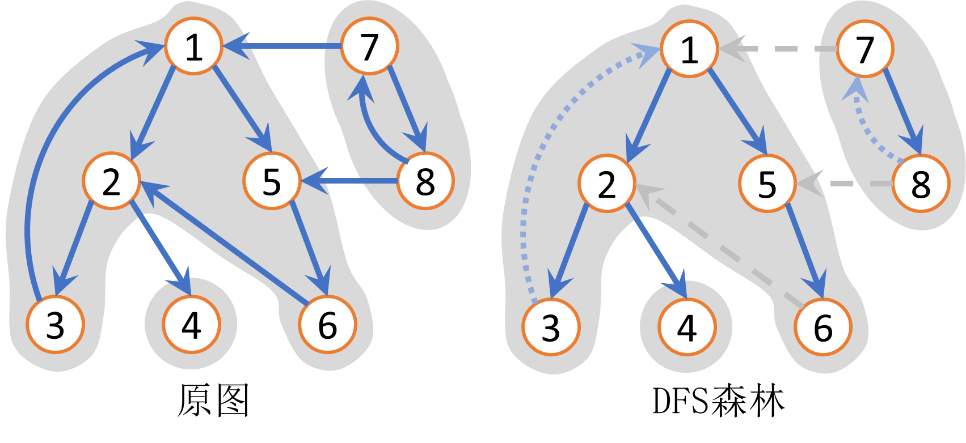
问题五、先在原图中 \(\texttt{DFS}\) 获得森林,利用找的的根在反图中 \(\texttt{DFS}\) 时, 能保证不会从一个树遍历到另一棵树中吗?
原图中 \(\texttt{DFS}\) 时给每个结点记录离开时间戳, 按照离开时间戳从大到小在反图中 \(\texttt{DFS}\), 不会遍历到其他树中。
通过上面的思考我们可以设计求有向图的强连通分量的算法(\(\texttt{Kosaraju}\) 算法)
这个算法可以说是最容易理解,最通用的算法,其比较关键的部分是同时应用了原图 \(G\) 和反图 \(GT\)。
先用对原图 \(G\) 进行深搜形成森林(树),并按照记录每个结点的离开时间将结点排列起来。
然后按照排列好的点,取最后的点为根对其在反图中进行深搜,摘除能遍历到的结点就是一个强连通分量。
余下部分再从排列好的点中取未摘除的最后的点继续步骤 \(2\) 直到没有顶点为止。
\(\texttt{Kosaraju}\) 代码
#include <iostream>
#include <stack>
#include <cstdio>
#include <cstring>
using namespace std;
int map[511][511], nmap[511][511], vist[501], N;
stack<int> S;
int DFS1( int v ) { //在原图中DFS,并在离开时入栈(时间戳)
vist[v] = 1;
for ( int i = 1; i <= N; i++ )
if ( !vist[i] && map[v][i]) DFS1( i );
S.push( v );
return 0;
}
int DFS2( int v, int &t) { // 在反图中DFS
vist[v] = t;
for ( int i = 1; i <= N; i++ )
if ( !vist[i] && nmap[v][i]) DFS2(i,t);
return 0;
}
int kosaraju() {
while ( !S.empty() ) S.pop(); // 清空栈
memset( vist, 0, sizeof(vist) );
for ( int i = 1; i <= N; i++ )
if ( !vist[i] ) DFS1( i ); //未被遍历过,调用DFS遍历
int t = 0;
memset( vist, 0, sizeof(vist) );
while ( !S.empty() ) {
int v = S.top(); //出栈顺序既是离开结点时间戳倒序
S.pop();
printf( "|%d|", v );
if ( !vist[v] ) {
t++;
DFS2(v, t); //按离开结点时间戳倒序在反图中DFS
}
}
return t;
}
int main() {
int M, i, s, e;
scanf( "%d%d", &N, &M );
memset( map, 0, sizeof(map) );
memset( nmap, 0, sizeof(nmap) );
for ( i = 0; i < M; i++ ) {
scanf( "%d%d", &s, &e );
map[s][e] = 1;
nmap[e][s] = 1;
}
printf( "%d\n", kosaraju() ); /* 输出连通分量个数 */
return 0;
}
\(\texttt{Tarjan}\) 算法原理
\(\texttt{Tarjan}\) 算法是基于深度优先搜索的算法,是图论中非常实用的算法之一。它可以在线性时间内求出有向图强连通分量、无向图双连通分量、无向图割点和桥、最近公共祖先(\(\text{LCA}\))等问题。
思考: 有向图 \(G\) 某个强连通分量中的所有结点,一定都在图 \(G\) 深搜树以某个结点为根的子树中吗?
一定,只要深搜到其强连通分量中的任一结点 ,由于强连通分量的性质, 以该点为根一定可以遍历到这个强连通分量中的所有结点。
那么其实,我们 只要确定每个强连通分量中的根结点,然后 根据这些根从树的最低层开始,一个一个的拿出强连通分量即可。那么剩下的问题就只剩下如何确定强连通分量的根和如何从最低层开始拿出强连通分量了。
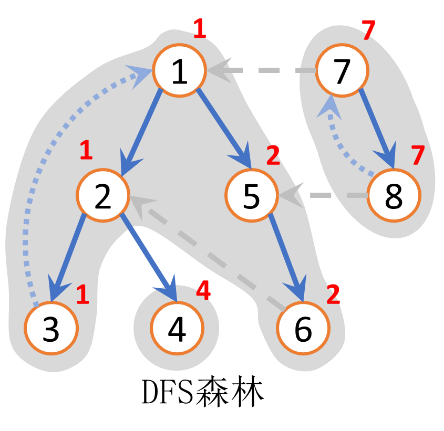
观察上图,找到强连通分量的根的特点。这里需要两个辅助数组 \(\texttt{dfn}\)(结点内数字)和 \(\texttt{low}\)(节点上数字)。
开始时间戳 \(\texttt{dfn}\): 是用来标记图中每个结点在进行深度优先搜索时被访问到的顺序序号。
性质:
- 祖先的 \(\texttt{dfn}\) 总比子孙的 \(\texttt{dfn}\) 小;
- 先生成的子树(左边的子树)中的结点总比后生成的子树(右边的子树)中的结点的 \(\texttt{dfn}\) 小。
追溯时间 \(\texttt{low}\) :\(\texttt{low[u]}\) 记录 \(u\) 子树内回弧或横叉弧指向的所有结点中最小的 \(\texttt{dfn}\) 值。这里需要加一个限制,已经深搜结束的强连通分量不能被指向。
问题一、不在 \(\texttt{dfs}\) 树上的弧 \((u,v)\)(\(u\) 指向 \(v\)),既横叉弧及回弧,开始时间戳 \(\texttt{dfn[u]}\) 与 \(\texttt{dfn[v]}\) 值的关系是?
\(\texttt{dfn[u]>dfn[v]}\)
问题二、如果 \(u\) 是某个强连通分量的根,那么 \(u\) 及其子树中的结点,存在回边指向 \(u\) 吗?存在回边指向 \(u\) 的祖先结点吗?
一定存在回边指向 \(u\), 保证子树内结点与 \(u\) 互相可达。 不存在指向 \(u\) 祖先的回边。如果可以返回到 \(u\) 的祖先 \(v\),那么 \(v\) 到 \(u\) 及 \(u\) 到 \(v\) 都有路径,则 \(u\) 和 \(v\) 属于同一强连通分量,与假设的 \(u\) 是强连通分量的根不符。
问题三、前文已经提到横叉弧只会从后遍历到的结点指向先遍历到的结点,那么先 \(\texttt{dfs}\) 遍历完的强连通分量内, 会有横叉弧指向后遍历到的强连通分量中的结点吗?反之,后遍历到的强连通分量会有横叉弧指向先遍历到的强连通分量中的结点吗?强连通分量内的结点间会有横叉弧吗?
强连通分量间的横叉弧,只可能是后遍历的分量指向先遍历的分量。强连通分量内的结点间也会有横叉弧。
问题四、如何 判断横叉弧的两个结点是否属于同一个强连通分量?
在遍历到某个结点 \(u\),存在横叉弧指向 \(v\) 时:
- 如果 \(v\) 所在分量没有遍历结束(即退出其强连通分量的根),说明 \(v\) 所在分量的根 \(r\) 是 \(u\) 的祖先节点,\(r\) 至 \(u\) 有路径,\(u\) 也可以借助 \(v\) 连通 \(r\),那么 \(u\) 与 \(v\) 属于同一个分量。
- 如果 \(v\) 结点所在分量已经遍历结束, 说明 \(v\) 所在分量的根,没有路径可达 \(u\),那么 \(u\) 和 \(v\) 不属于一个分量。
问题五、如何判断结点 \(u\) 是某个强连通分量的根?
\(\texttt{low[u]==dfn[u]}\)
\(\texttt{Tarjan}\) 算法代码
struct ENode{int v,w,p;}e[MAXM]; //边集
int h[MAXN],ec; //点集和边集计数
void AddEdge(int u, int v, int w){ //插入边
e[++ec].v = v; e[ec].w = w;
e[ec].p = h[u]; h[u] = ec;
}
int dfn[MAXN],tc,low[MAXN]; //时间戳,时间戳计数,祖先时间。
int gid[MAXN],gc; // 分量数组,分量计数。
bool ins[MAXN]; stack<int> sTar; //入栈标志,辅助栈
void Tarjan(int u){
dfn[u]=low[u]=++tc; //时间戳与祖先时间初始化
ins[u]=1; sTar.push(u); //入栈
for(int i=h[u];i;i=e[i].p){ //递归处理所有子结点
int v=e[i].v;
if(!dfn[v]){
Tarjan(v);
low[u]=min(low[u],low[v]);
//更新low[u],表示子树内结点能回指的最早祖先时间戳
}
else if(ins[v])//如果是回边或横叉边,更新追溯时间low[u]
low[u]=min(low[u],dfn[v]);
}//dfn[v],可改为low[v],求桥时也可以,但求割点时不可以。
if(low[u]==dfn[u]){ //判断U是否分量的根
gc++;
int i;
do{
i=sTar.top(); ins[i]=0;
gid[i]=gc; sTar.pop(); //分量出栈
}while(i!=u); //出栈至当前结点,包括当前结点
}
}
题目描述
现在给出一个有向图。结点个数 \(N(<=1000)(\)编号 \(1 \sim N)\),边数 \(M(<=5000)\)。请你按照从小到大的顺序输出最大的强连通分量所有的结点编号。
格式
输入格式
第一行 \(N\) 和 \(M\);
以下 \(M\) 行,每行两个空格隔开的整数表示一条有向边。
输出格式
输出一行,最大的强连通分量的结点编号(由小到大输出)。
样例1
样例输入1
10 20
2 2
5 3
8 5
3 4
8 7
10 10
10 6
7 7
2 8
3 2
8 1
3 8
1 7
8 10
7 5
6 4
9 2
8 6
7 5
1 8
样例输出1
1 2 3 5 7 8
限制
时间:\(1s\) 空间:\(256M\)
对于 \(50\%\) 的数据:\(N<=1000, M<=5000\);
对于 \(100\%\) 的数据:\(N<=50000, M<=200000\);
\(\texttt{Windows}\) 下需要开栈;
来源
地址:\(zloj,J2020\)域
作者:\(jialiang2509\)