测试数据来自 oistream/1142

背景

• Idea: 北京市赛
• Data: 暂无
• Std: 北京市赛
• 题面: 北京市赛+oistream

描述

你有 \(q\) 组询问，每组询问你需要计算出组合数 \(\dbinom{n}{m}\) 的因子数量。

\(\dbinom{n}{m}\) 表示 \(n\) 个互不相同的球中取 \(m\) 个球的方案数，也就是

\[\dbinom{n}{m}=\dfrac{n!}{m!(n-m)!}\]

由于答案可能很大，你只需要输出将答案对 \(p=10^9+7\) 取模的结果即可。

输入格式

• 第一行一个正整数 \(q\) 表示询问数量。
• 接下来 \(q\) 行，每行 \(2\) 个整数 \(n,m\)，保证 \(0\leq m\leq n\)。

输出格式

输出 \(q\) 行，每行一个整数对应该询问的答案。

样例

输入样例1

3
0 0
4 2
10 3

输出样例1

1
4
16

样例解释1

• \(\dbinom{0}{0}=1\)，有 \(1\) 个因子。
• \(\dbinom{4}{2}=6\)，有 \(4\) 个因子：\(\{1,2,3,6\}\)。
• \(\dbinom{10}{3}=120\)，有 \(16\) 个因子：\(\{1,2,3,4,5,6,8,10,12,15,20,24,30,40,60,120\}\)。

输入样例2

见附加文件。

输出样例2

见附加文件。

数据规模与约定

对于 \(100\%\) 的数据，保证 \(n\leq 10^5,q\leq 10^5\)。

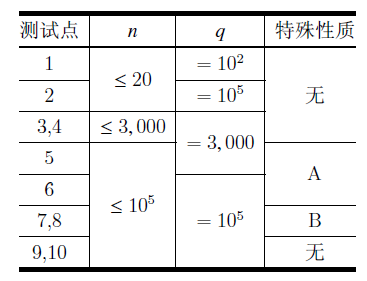
• 特殊性质 \(\text{A}\)：保证 \(\dbinom{n}{m}\leq 10^6\)。
• 特殊性质 \(\text{B}\)：保证输入的 \(n\) 值总是同一个数。