测试数据来自 nnu_contest/1321

Limits

时间限制：2000ms

内存限制：512MB

Description

漆黑的晚上，小F躺在床上辗转反侧。难以入眠的他想起了今天下午他的一次悲惨的月赛比赛经历。那是一道“基础”的关于lowbit与highbit的题目：

给定一个n位的针对正整数\(x\)的0-1操作序列，其中0表示\(x+=lowbit(x)\)，1表示\(x+=highbit(x)\)，其中\(highbit(x)\)为该数在二进制表示下的最高二进制位的位值，\(lowbit(x)\)为该数在二进制表示下的最低非零二进制位的位值，例如

\(highbit(22_{(10)})=highbit(10110_{(2)})=10000_{(2) })=16_{(10)}\)

\(lowbit(22_{(10)})=lowbit(10110_{(2)})=10_{(2)})=2_{(10)}\)

现在给出\(q\)个正整数\(x_1..x_q\)(均在\([1,2^{30}]\)之间)，对\(x_i\)依次应用操作序列中\([l_i,r_i]\)(这个区间由数据给出)的操作，求操作后的\(q\)个数对\(10^9+7\)取模的余数。\((1≤n,q≤10^5)\)

尽管此时的小F非常的simple，但是他还是发现这题可以争取部分分数。非常young的他写了一个模拟二进制高精度来解决这个问题，其复杂度\(O(nq)\)显然不能得满分。不过，他注意到了一个性质：

对于满足\(x=2^a (a∈N,下同)\)形式的数，有\(lowbit(x)=highbit(x)=x\)。

这意味着某些数据经过若干步的模拟操作后，将变成\(x=2^a\)的形式，然后任何操作都变成乘2，这使得小F可以优化他的算法。然而，由于学院辅导员突然打来电话要他去办公室处理一些问题，小F不得不终止比赛。赛后，小F测试了这种方法，发现可以获得整题一半的分数，这让他非常难过。

尽管这样的方法得不到满分，但是小F还是想要算一下，在区间\([2^m,2^n]\)内，有多少个数能够在给定的0-1操作序列中截取一段长度不超过\(k\)的区间并依次应用区间中所有操作后，能够变成\(2^a\)的形式？当然，总数量可能太大，因此请输出答案除以\(10^9+7\)的余数。

注意：若一个数无需任何操作即满足\(2^a\)的形式，也在我们的统计范围内。

Input

第1行，4个整数\(m,n,k,d\)。其中，\(m,n,k\)含义见上，\(d\)表示操作序列的长度。

第2行，一个0-1字符串，表示操作序列。

Output

一个数，表示\([2^m,2^n]\)中可以按要求转化为\(2^a\)的形式的数的数量除以\(10^9+7\)的余数。

Samples

Sample Input

1 3 2 3
101

Sample Output

6

Explanation

操作序列“101”共有5个本质不同的操作区间，分别为1,0,10,01,101，由于\(k=2\)，合法的本质不同的操作区间只有1,0,10,01，共四个。

在\([2^1,2^3]\)中，2,4,8不经任何操作即为\(2^a\)的形式；

3,6,7只需1次“0”操作\((x+=lowbit(x))\)即可变成\(2^a\)的形式；

5经过上述任何一个合法的操作区间的操作后均不能变成\(2^a\)的形式；

因此答案为6。

Data range

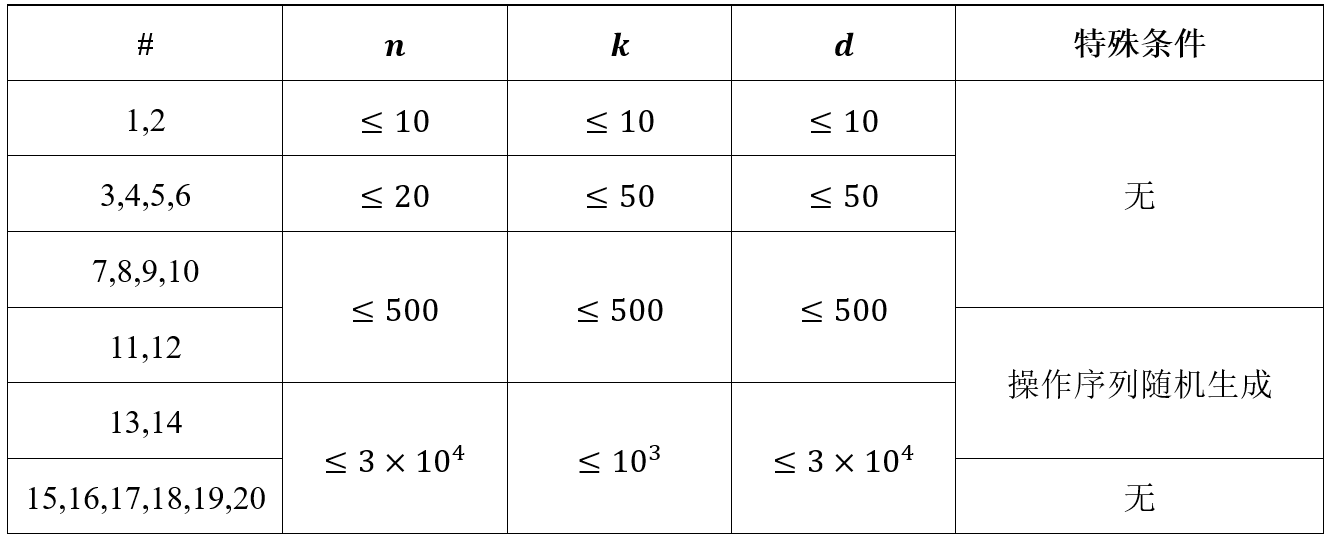
对于100%的数据，\(1≤m≤n≤3×10^4,1≤k≤1000,1≤d≤3×10^4,k≤d\)。

• 由于本题的复杂度可以做到更优，新增5组数据，#21~#25满足 \(1\le m,n \le 10^9, 1\le k\le d\le 10^6\)