逛公园
测试数据来自 system/2030
描述
策策同学特别喜欢逛公园。公园可以看成一张 \(N\) 个点 \(M\) 条边构成的有向图,且没有自环和重边。其中 \(1\) 号点是公园的入口,\(N\) 号点是公园的出口,每条边有一个非负权值,代表策策经过这条边所要花的时间。策策每天都会去逛公园,他总是从 \(1\) 号点进去,从 \(N\) 号点出来。
策策喜欢新鲜的事物,他不希望有两天逛公园的路线完全一样,同时策策还是一个特别热爱学习的好孩子,他不希望每天在逛公园这件事上花费太多的时间。如果\(1\)号点到\(N\)号点的最短路长为\(d\),那么策策只会喜欢长度不超过\(d+K\)的路线。策策同学想知道总共有多少条满足条件的路线,你能帮帮他吗?
为避免输出过大,答案对\(P\)取模。如果有无穷多条合法的路线,请输出\(-1\)。
格式
输入格式
第一行包含一个整数 \(T\), 代表数据组数。接下来\(T\)组数据,对于每组数据:
第一行包含四个整数 \(N\), \(M\), \(K\), \(P\),每两个整数之间用一个空格隔开。
接下来\(M\)行,每行三个整数\(a_i\), \(b_i\), \(c_i\),代表编号为\(a_i\), \(b_i\)的点之间有一条权值为 \(c_i\)的有向边,每两个整数之间用一个空格隔开。
输出格式
输出文件包含 \(T\) 行,每行一个整数代表答案。
样例1
样例输入1
2
5 7 2 10
1 2 1
2 4 0
4 5 2
2 3 2
3 4 1
3 5 2
1 5 3
2 2 0 10
1 2 0
2 1 0
样例输出1
3
-1
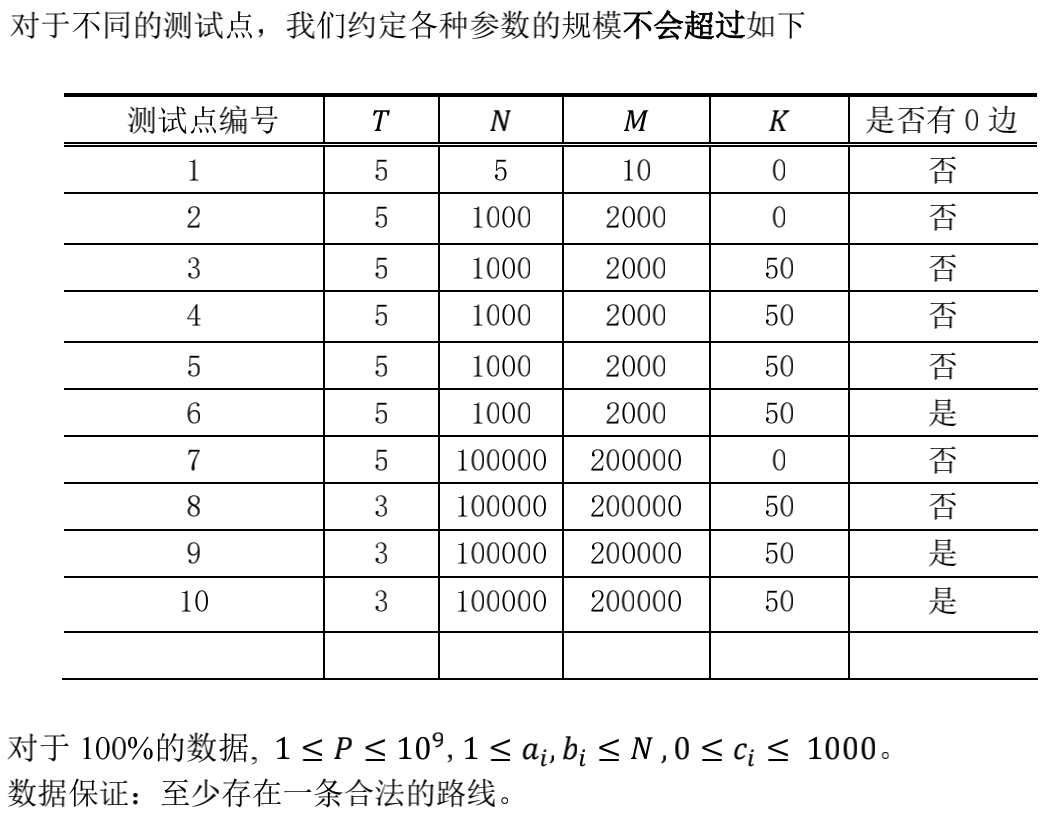
限制
信息
- ID
- 1011
- 难度
- 10
- 分类
- (无)
- 标签
- 递交数
- 3
- 已通过
- 0
- 通过率
- 0%
- 上传者