暂无测试数据。

加强说明

数据较 原题 与 加强版 \(1\) 再有所加强，请 关注数据范围 。题面 大体 相同，在加强版 \(1\) 的基础上新增一组大样例。实际上本题与 \(\text{SP26073 DIVCNT1 - Counting Divisors}\) 基本相同。

题目描述

科学家们在 \(\text{Samuel}\) 星球上的探险得到了丰富的能源储备，这使得空间站中大型计算机 \(\text{Samuel II}\) 的长时间运算成为了可能。由于在去年一年的辛苦工作取得了不错的成绩，小联被允许用 \(\text{Samuel II}\) 进行数学研究。

小联最近在研究和约数有关的问题，他统计每个正数 \(N\) 的约数的个数，并以 \(f(N)\) 来表示。例如 \(12\) 的约数有 \(1,2,3,4,6,12\)，因此 \(f(12)=6\)。下表给出了一些 \(f(N)\) 的取值：

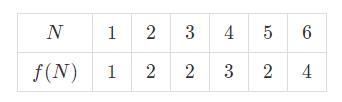
\(T\) 组询问 ，现在请你求出：

\[\sum_{i=1}^n f(i)\]

输入格式

第一行一个整数 \(T\)，表示询问组数。
第二行 \(T\) 个整数 \(n\)，表示当前询问。

输出格式

一行 \(T\) 个整数表示答案，空格隔开。

样例输入

4
3 233333 233333333333 233333333333333333

样例输出

5 2920097 6143705216087 9367324346587466041

样例解释

\(f(1) + f(2) + f(3) = 1 + 2 + 2 = 5\).

数据范围

对于 \(30 \%\) 的数据，\(T \leq 1 , N \leq 10^{15}\).
对于 \(60 \%\) 的数据，\(T \leq 10^3 , N \leq 10^{15}\).
对于 \(80 \%\) 的数据，\(T \leq 10^4 , N \leq 10^{18}\).
对于 \(100 \%\) 的数据，\(1 \leq T \leq 10^5 , 1 \leq N < 2^{63}\).

说明 / 提示

本题答案有可能爆 \(\text{long long}\).