题目描述

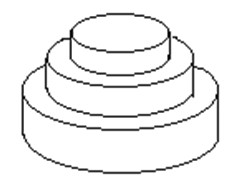
Mr.W 要制作一个体积为 $N\pi$ 的 $M$ 层生日蛋糕，每层都是一个圆柱体。
设从下往上数第 $i$ 蛋糕是半径为 $R_i$，高度为 $H_i$ 的圆柱。当 $i<M$ 时，要求 $R_i>R_{i+1}$且 $H_i >H_{i+1}$。由于要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积 $Q$ 最小。
令 $Q =Sπ$ ，请编程对给出的 $N$ 和 $M$ ，找出蛋糕的制作方案（适当的 $R_i$ 和 $H_i$ 的值），使 $S$ 最小。（除 $Q$ 外，以上所有数据皆为正整数）

输入格式

第一行为 $N$ ，表示待制作的蛋糕的体积为 $N\pi$；

第二行为 $M$ ，表示蛋糕的层数为 $M$ 。

输出格式

输出仅一行，一个整数 $S$（若无解则 $S=0$ ）。

样例数据

样例输入

100
2

样例输出

68

附：圆柱相关公式：体积 $V=\pi R^2H$；侧面积 $S’=2\pi RH$；底面积 $S=\pi R^2$。

限制与提示

对于全部数据，$1 \leq N \leq 10^4,1 \leq M \leq 20$。