暂无测试数据。

古老数据结构

题目背景

在公元前 2026 年，第 -64 届全国青少年信息学奥林匹克冬令营前夕，墨子找到了一位来自 6202 年的人，他给了墨子第 43 届冬令营的题目来练习。

他打开了第三题 “古老数据结构” 这道题目：

你需要实现一个用来动态维护树的结构支持删除点并在线性时间内返回直径的数据结构。

墨子想了一下，决定造一台 2026 年的计算机来试着运行这个题目，他手搓了一个 2026 年的编译器，并很快得到了结果……

这时你从梦中惊醒，发现自己居然在第 43 届冬令营赛场上。之前的一切只是南柯一梦，而自己正需要解决“古老数据结构”这道题目。

然而你已经记不清梦中的程序运行的结果了，你试图与梦中的墨子沟通。但是他并不想帮助你，他只会给你他维护的步骤，而你仍然需要他所给的步骤求出答案。

题目描述

墨子维护了一棵多叉树。

这棵多叉树在初始时刻有 \(n\) 个节点，墨子的每次修改如下：

墨子会使用这个数据结构找到树上所有的点，并将任意至少一条直径经过节点加入集合 \(s\) 。

• 每一次操作，他会将 \(s\) 集合里所有的节点标记为该点的深度累加到答案中。

• 墨子会删除这些节点中在所有直径中的点（除了根节点），如果这个点不是叶子节点，他会将这一个点的儿子与根连接。

• 特别的如果树上只有一个节点，则这个节点会被墨子直接删掉并累加。

你需要输出在操作结束后所有节点被标记的值。

输入格式

输入共 \(n\) 行。

第一行一个整数 \(n\)，表示初始节点个数。

接下来 \(n−1\) 行每行两个整数 \(u,v\) 表示 \(u\) 和 \(v\) 之间有一条连边。

输出格式

共一行，\(k\) 个整数表示每次删除后共计的答案。

输入输出样例 #1

输入 #1

10
1 2
1 3
4 2
5 2
3 6
4 7
7 8
5 9
10 5

输出 #1

19 27 28

说明/提示

样例解释

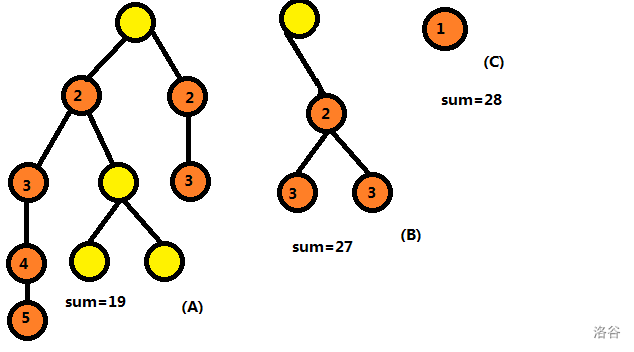
第一次选定节点 \(2,3,4,6,7,8\) ，深度和为 \(19\) 。

将独立的儿子 \(5\) 连接节点 \(1\) 。

第二次选定节点 \(5,9,10\) , 深度和为 \(8\) , 共计 \(27\) 。

仅剩下的节点 \(1\) 在最后一次被删除，深度共计 \(28\) 。

数据范围

对于 \(78\%\) 的数据，有 \(N \le 10^4\) 。

对于 \(100\%\) 的数据，有 \(N \le 10^6\) 。