题目背景

NOIP 2000 提高组 T4

题目描述

设有 \(N \times N\) 的方格图，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字 \(0\)。如下图所示（见样例）:

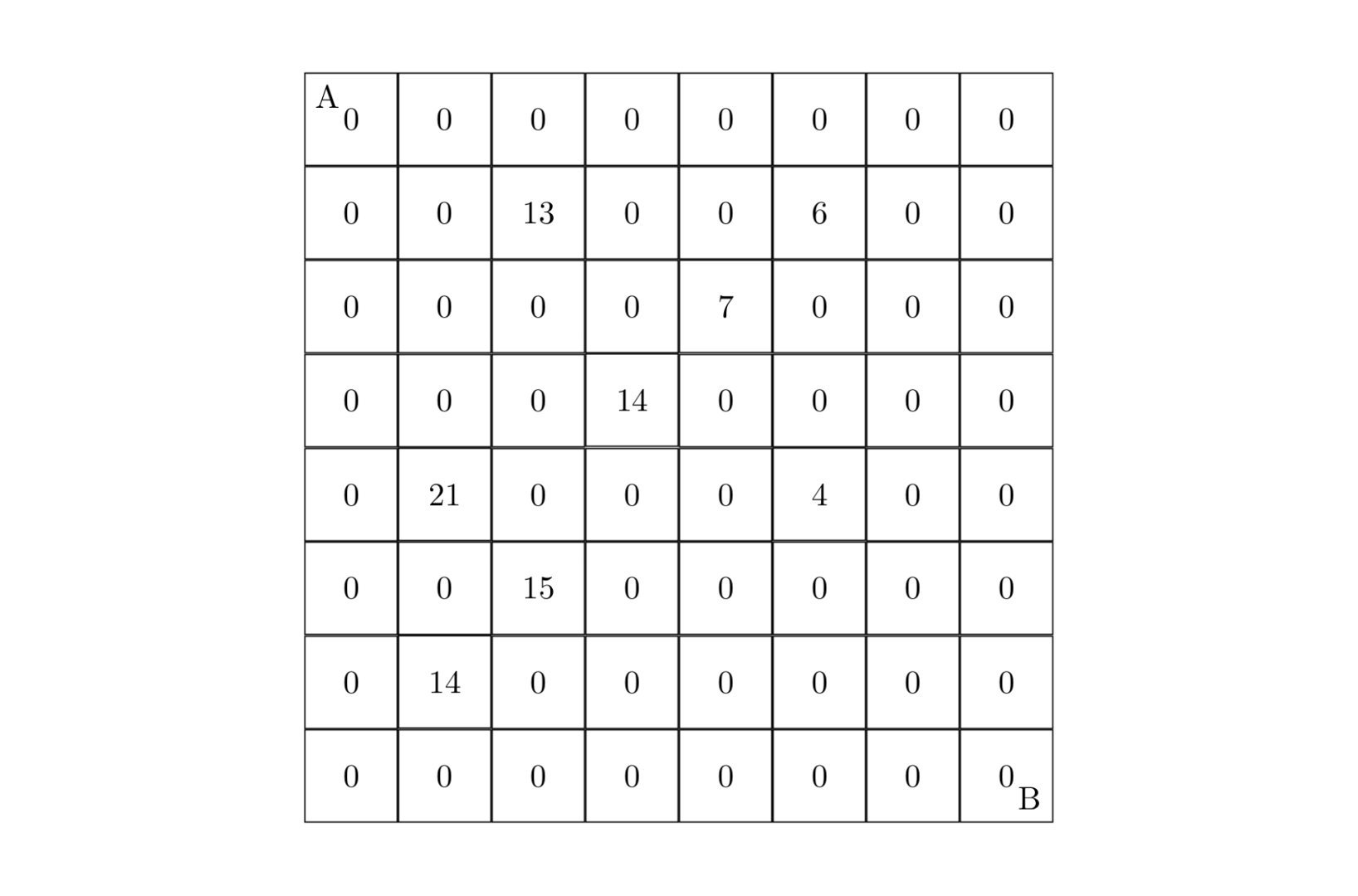
某人从图的左上角的 \(A\) 点出发，可以向下行走，也可以向右走，直到到达右下角的 \(B\) 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 \(0\)）。

此人从 \(A\) 点到 \(B\) 点共走两次，试找出 \(2\) 条这样的路径，使得取得的数之和为最大。

输入格式

输入的第一行为一个整数 \(N\)（表示 \(N \times N\) 的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的 \(0\) 表示输入结束。

输出格式

只需输出一个整数，表示 \(2\) 条路径上取得的最大的和。

样例 #1

样例输入 #1

8
2 3 13
2 6  6
3 5  7
4 4 14
5 2 21
5 6  4
6 3 15
7 2 14
0 0  0

样例输出 #1

67

提示

【数据范围】

对于 \(10\%\) 的数据，满足 \(1\le N\le10\)。
对于 \(50\%\) 的数据，满足 \(1\le N\le50\)。
对于 \(100\%\) 的数据，满足 \(1\le N\le10^2\)，每个方格的数字在 \([0,10^5]\) 范围内。

【时空限制】

时间限制：\(1\,\rm s\)。

空间限制：\(128\,\rm MiB\)。