测试数据来自 system/1800

描述

在遥远的未来，食物将会通过两个星球之间的单向通道传输，每条通道连接两个星球，食物通过这条通道需要一定的时间。
工商协会计划利用一项最近发明的技术——超时空传送来开辟一些新的传输通道。超时空传送也是单向的。至今为止，超时空传送所需的时间仍然是未知的，但已知的是超时空传送所需的时间不由路程决定，因此通过每一条超时空传送通道的所需时间是相等的。
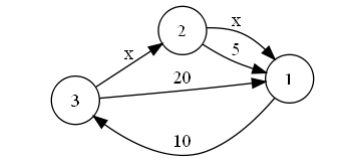
下图展示了一个包含三个连通的星球的例子。星球用正整数标号，通过超时空传送通道所需的时间用“x”表示。（下图为样例二）

通道的通过时间都是以天为单位的正整数。
工商协会希望你来分析开辟这些新通道后，对于每个可能的x的值，从星球A到星球B的最短路径耗费的时间。例如，在上图中，如果x≥ 5，从星球2到星球1花费的时间为5天，如果x<5，耗费的时间可能是4天，3天，2天或1天。

格式

输入格式

第一行为两个整数P和R(1 ≤ P ≤ 500, 0 ≤ R ≤ 10 000)，表示星球的总数和通道的总数。
接下来的第2行到第R+1行，每行三个整数C，D，T (1 ≤ C, D ≤ P, C ≠ D)，对于常规通道，T是一个整数(1 ≤ T ≤ 1 000 000)，对于超时空传送通道来说，T是字符“x”，两个星球间可能有多条道路。
第R+2行是一个整数Q(1 ≤ Q ≤ 10)，为查询的个数。
接下来的第R+3行到第R+Q+2行，每行两个整数A和B，表示查询对于每个可能x值，从星球A到星球B的最短距离耗费的时间一共有多少种，以及它们的总和。

输出格式

输出一共包括Q行，每一行为两个正整数，表示从星球A到星球B的最短距离耗费的时间一共有多少种和它们的总和。如果可能有无限多种，输出“inf”，如果两个星球间没有通道，则耗费时间的种数及它们的总和都为0.

样例1

样例输入1

4 4 
1 2 x 
2 3 x 
3 4 x 
1 4 8 
3 
2 1 
1 3 
1 4

样例输出1

0 0 
inf 
3 17 

样例2

样例输入2

3 5 
3 2 x 
2 1 x 
2 1 5 
1 3 10 
3 1 20 
6 
1 2 
2 3 
3 1 
2 1 
3 2 
1 3 

样例输出2

inf 
5 65 
15 185 
5 15 
inf 
1 10

限制

各个测试点1s