题目传送门

这是一道裸的01背包，不懂01背包的同学建议大家可以看一下教程

~~如果是已经学会的大佬请跳过~~

给定n种物品，每种物品都有重量wi和价值vi，每种物品只有一个。另外，背包容量为W。求解在不超过背包容量的情况下将哪些物品放入背包，才可以使背包中的物品价值之和最大。每种物品只有一个，要么不放入（0），要么放入（1），因此称之为01背包。
假设第i阶段表示处理第i种物品，第i-1阶段处理第i-1种物品，则当处理第i种物品时，前i-1中物品已经处理完毕，只需考虑第i-1阶段向第i阶段的转移。
状态表示：c[i][j]表示将前i种物品放入容量为j的背包中获得的最大价值。
第i种物品的处理状态包括以下两种
（1）不放入：放入背包的价值不增加，问题转化为“将前i-1种物品放入容量为j的背包中获得的最大价值”，最大价值为c[i-1][j]
（2）放入：在第i种物品放入之前为第i-1阶段，相当于从第i-1阶段向第i阶段转化。问题转化为“将前i-1种物品放入容量为j-w[i]的背包中获得的最大价值”，此时获得最大价值就是c[i-1][j-w[i]],再加上放入第i种物品获得的价值v[i]，总价值为c[i-1][j-w[i]]+v[i]
注意：若背包容量不足，则肯定不可以放入，所以仍为前i-1种的物品处理后的结果：若背包容量充足，则考察在放入、不放入哪种情况下获得的最大价值更大。

状态转移方程：
if (j < w[i])
c[i][j] = c[i-1][j];

else c[i][j] = max(c[i-1][j], c[i-1][j-w[i]]+v[i]);

算法步骤

1）初始化

c[0][j]=0,c[i][0]=0,其中i=0,1,2,…,n,j=0,1,2,…,W，表示第0种物品或背包容量为0时获得的价值为0；

2）循环阶段

(1) 按照状态转移方程处理第1种物品，得到c[1][j],j=1,2,…, W
(2)按照状态转移方程处理第2种物品，得到c[2][j], j=1,2,…, W.
(3)依次类推，得到c[n][j],j=1,2,…w.

3)构造最优解

c[n][W]就是不超过背包容量时可以放入物品的最大价值（最优值）。若还想知道具体放入了哪些物品，则根据c[][]数组逆向构造最优解。对此可以用一维数组x[]来存储解向量，x[i]=1表示第i种物品被放入背包，x[i]=0表示第i种物品未被放入背包。

(1)初始时i=n,j=W。

(2)若c[i][j]>c[i-1][j],则说明第i种物品被放入背包，令x[i]=1,j-=w[i];若c[i][j]<=c[i-1][j],则说明第i种物品没被放入背包，令x[i]=0。

(3)i--,转向第2步，直到 i=1时处理完毕。
此时已经得到解向量（x[1],x[2],…,x[n]），直接输出该解向量，也可以仅把x[i]=1的物品序号i输出。

算法代码：

推理过程请看图解：

回归正题，二维dp代码如下：
cpp
//Lucas Ray
#include <bits/stdc++.h>
#define long long int
using namespace std;
const int maxn = 110;
int t, m, ans = 0;
int v[maxn], w[maxn], dp[maxn][maxn*10]; //v代表时间（即花费），w代表价值
int main() {
scanf ("%d%d", &t, &m);
for (int i = 1; i <= m; i++) {
scanf ("%d%d", &v[i], &w[i]);
}
for (int i = 1; i <= m; i++) {
for (int j = t; j >= 0; j--) {
if (j >= v[i]) {
dp[i][j] = max(dp[i-1][j-v[i]]+w[i], dp[i-1][j]);
} else {
dp[i][j] = dp[i-1][j];
}
}
}
printf ("%d", dp[m][t]);
return 0;
}


二维dp AC记录

有的大佬看到这里就会说了：你这么菜啊，连一维优化都不会啊

算法优化！！！

状态表示：dp[j]表示将物品放入容量为j的背包中可以获得的最大价值。

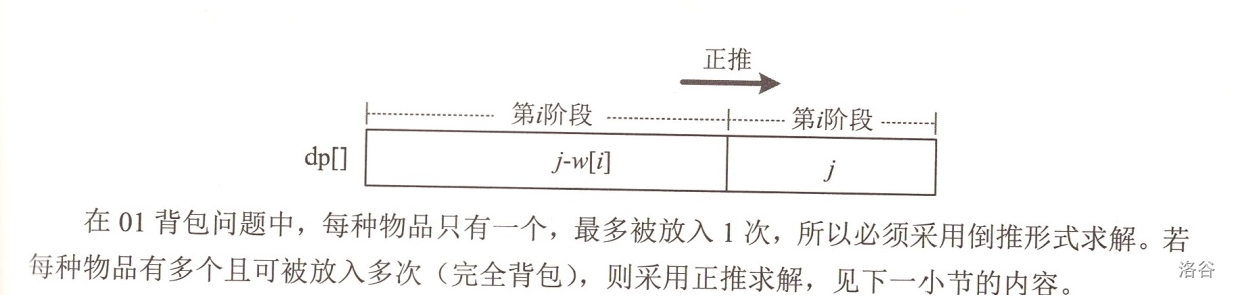
那就来看一维优化的代码吧

//Lucas Ray
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 3;
int dp[maxn];
int n, m;
int times[maxn], val[maxn];
inline int read() { //快读
    char a;
    int c=0,y=1;
    a=getchar();
    while(a<'0'||a>'9')
    {
        if(a=='-')
        {
            y=-1;
        }
        a=getchar();
    }
    while(a>='0'&&a<='9')
    {
        c=c*10+a-'0';
        a=getchar();
    }
    return c*y;
}
int main() {
    n = read(), m = read();
    for (int i = 1; i <= m; i++) {
        times[i] = read(), val[i] = read();
    }
    for (int i = 1; i <= m; i++) {
        for (int j = n; j >= 0; j--) {
            if (j >= times[i])
            dp[j] = max (dp[j], dp[j-times[i]] + val[i]);
        }
    }
    cout << dp[n] << endl;
    return 0;
}

这是蒟蒻发的第一篇题解，制作不易，不喜喷轻点