题目描述

有一个含\(n\)个点的无向图，这个图本身是未知的，但你知道关于它的一些信息（下文中点的标号从1开始计数）：
* 它是一个简单无权图，也就是说，它没有重边自环，所有边的权均为1；
* 从1号点到任意点的最短路都是唯一的。设\(l_i\)是从1号点出发到达\(i\)号点的最短路长度，你虽然不知道\(l_i\)具体是多少，但知道\(l_i\)关于\(i\)非严格单调递增。换句话说，对于\(2 \leq i \leq n\)，有\(l_{i-1} \leq l_i\)；
* 每个点的度（与之直接相连的边的个数）\(d_i\)都是给定的，且只可能是2或3。
你想知道共有多少个满足条件的无向图，由于答案可能很大，你只需给出答案模\({10}^9+7\)的值即可

输入格式

第一行一个正整数\(n\)；
第二行n个正整数依次表示每个节点的度\(d_1, d_2 \cdots d_n\)。

输出格式

一个非负整数，表示答案模\({10}^9+7\)的值。

样例1

输入

5
2 3 3 2 2

输出

2

样例2

输入

20
2 2 2 2 3 2 3 2 2 2 2 2 2 2 2 2 2 3 3 2

输出

82944

样例说明

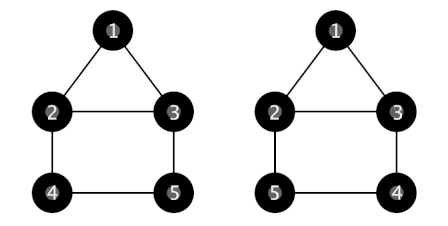
第一个样例对应以下两种情况：

数据规模、时空限制

对于30%的数据，\(n \leq 4\)
对于40%的数据，\(n \leq 5\)
对于100%的数据，\(3 \leq n \leq 50, \quad d_i \in \{ 2,3 \} \)
时间限制1s，空间限制512MB。

来源

2019.2 TYWZ提高组集训
供题人：于剑