题目描述

凭借自己出大价钱“请”的人气，李子明同学成功地登上了断罪小学大队长的宝座。为了答谢把他捧上宝座的弟兄们，也为了长期维持住自己的声望，李子明决定再投入一笔巨资，以“课外活动室”的名义，在校内托关系承包了一间小教室，并把它改造成弟兄们专属的棋牌厅兼游戏厅。
然而光有一间空屋子显然毫无意义，他还得再出一笔钱购买一些娱乐用品。他看中了\(N\)类物品，第\(i\)类物品的价格为\(p_i\)元/件，每件物品给玩家带来的“愉悦度”为\(v_i\)，\(i = 1,2 \cdots N\)。总的愉悦度等于购买的所有物品愉悦度之和。
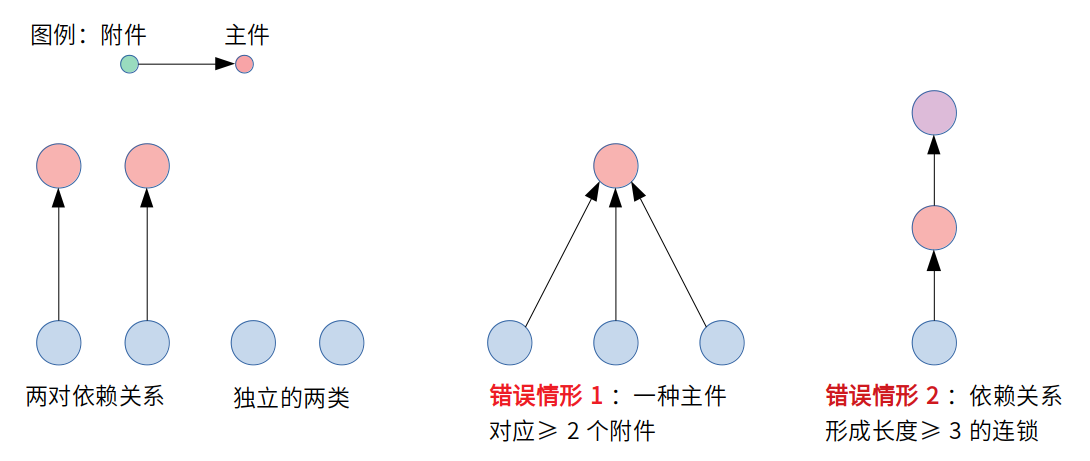
物品之间可能存在依赖关系，试想如果光买一个游戏手柄，却不买游戏主机，那显然是无法让人愉悦的。这\(N\)类物品中，某类物品可能是另外某一类物品的 附件 ，与附件对应的称为 “主件” 。规定：
* 附件的个数不得超过其主件的个数（否则多出来的附件毫无意义）；
* 如果A是B的附件，那么A一定不是其他任何一类物品的主件；
* 每一类物品至多可以是其他1类物品的主件。

由于经费有限，李子明只能出得起\(P\)元去采购物品。除去上述的依赖关系以外，每类物品购买的件数并没有其他任何限制。请你根据每种物品的单价、每件带来的愉悦度收益，以及物品间的依赖关系，编写程序求出李子明最多可以让“课外活动室”的玩家们获得多少愉悦度。

输入格式

第一行是一个正整数\(T\)，表示测试数据的组数。之后每组数据：
第一行是两个正整数\(N, P\)；
之后\(N\)行依次描述第\(1,2 \cdots N\)件物品的信息。每行包含3个整数\(p_i, v_i, d_i\)，其中\(p_i, v_i\)的含义见“题目描述”部分，\(d_i\)表示第\(i\)类物品为第\(d_i\)类的附件。若\(d_i = -1\)则表示第\(i\)类物品不是其他任何一种的附件，保证输入的所有\(d_i\)均满足上述3条规定。

输出格式

每组数据输出一行，在总花费不多于\(P\)元的前提下，愉悦度之和最大是多少。

样例

输入

2
4 20
4 25 -1
6 36 -1
2 24 1
3 30 2
3 20
7 50 -1
4 24 -1
1 3 1

输出

148
130

样例说明

第一组数据中，设四类物品选取的件数依次记为\(n_1, n_2, n_3, n_4\)，其中第3类是第1类的附件，第4类为第2类的附件，因此\(n_3 \le n_1, \quad n_4 \le n_2\)。
当\(n_1 = 4, \quad n_3 = 2,\quad n_2 = n_4 = 0\)时，总收益达到最大值148。

数据规模及约定

所有数据均满足：\(T \le 10, \quad N \le 100, \quad P \le 5 \times 10^4, \quad 1 \le p_i \le P, \quad 0 \le v_i \le 10^4\)
20%的数据满足：\(N \le 16\)
另外40%的数据满足：\(d_i = -1\)
时间限制1s，空间限制256MB。