Problem C. 树上的数

时间限制：2s

空间限制：256 MB

题目描述

给定一棵二叉树，每个点有点权 \(a_i\) 。

你可以执行若干次操作，每次操作你可以选择一个结点，并将这个结点的点权修改为 任意实数 。

问：至少进行多少次操作，才能使得这棵树变为 二叉排序树 ？

二叉排序树 是按照以下方法递归定义的。

若二叉树是空树，或满足以下要求，则它是二叉排序树。

• 左子树为空，或左子树上所有结点的点权 严格小于 它的根结点的点权。
• 右子树为空，或右子树上所有结点的点权 严格大于 它的根结点的点权。
• 左子树、右子树均为 二叉排序树 。

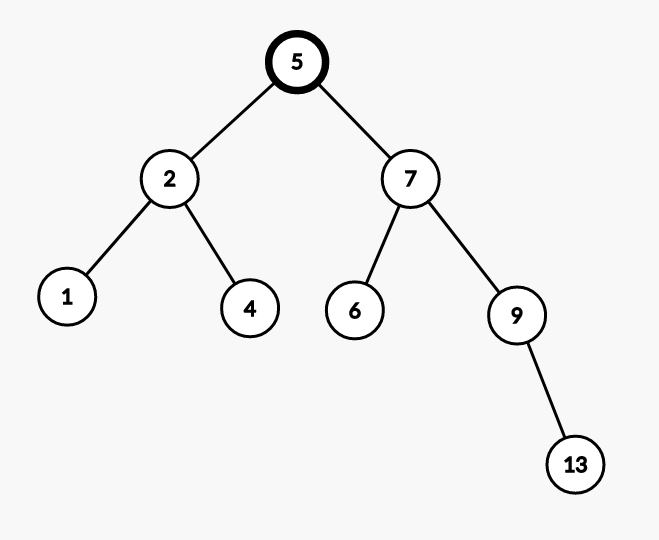
以下是一颗二叉排序树的例子（根结点的权值为 5），结点上的数字表示权值。

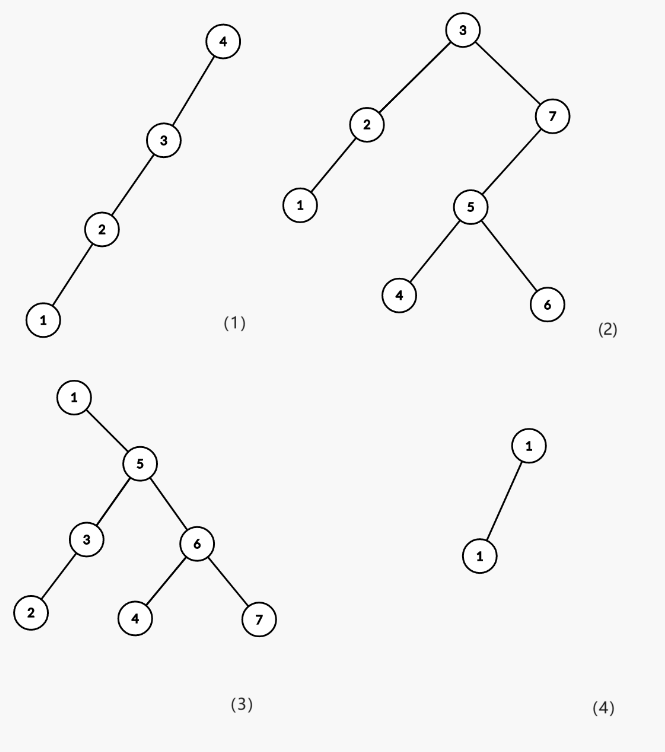
以下是更多例子。其中（1）（2）是二叉排序树，而（3）（4）不是。 因为（3）中 5 的右子树中存在值小于等于 5 的结点。（4）中 1 的左子树中存在值大于等于 1 的结点。

输入格式

第一行一个整数 \(n\)，表示二叉树的结点数和根结点编号。

第二行 \(n\) 个整数，表示每个点的点权 \(a_i\) 。

接下来 \(n\) 行每行两个整数\(l_{i}, r_{i}\)，其中第 \(i\) 行的两个整数分别表示第 \(i\) 个节点的左孩子 \(l_{i}\) 和右孩子\(r_{i}\) 。

如果该结点没有左孩子，则以 \(0\) 代替；

如果该结点没有右孩子，则以 \(0\) 代替。

输出格式

仅一个整数，表示最少需要的操作次数。

样例输入1

7 1
4 3 6 2 1 1 4
2 3
0 4
7 0
5 6
0 0
0 0 
0 0

样例输出1

3

样例1解释

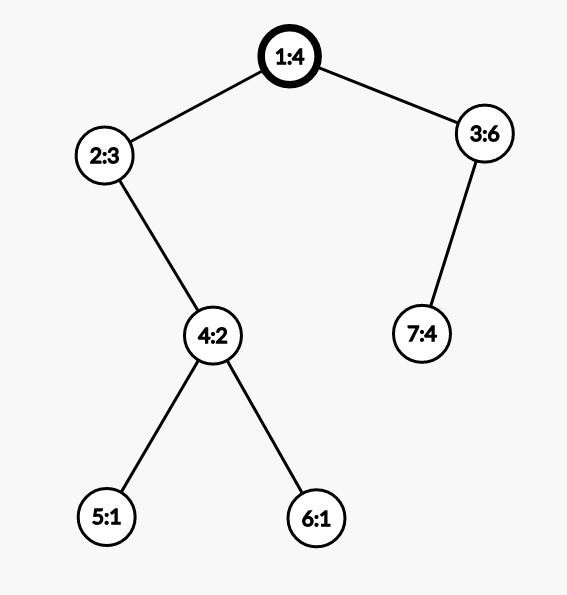
示意图

每个结点 X:Y 表示结点编号为 X，结点值为 Y。

其中一种修改方法为：

将 结点 2 的值改为 0

将 结点 6 的值改为 3

将 结点 7 的值改为 5

可以证明，至少需要三次修改，才能变为二叉排序树。

样例输入2

19 13
16 8 12 9 3 5 12 11 7 17 3 10 9 1 3 5 15 10 2 
19 0
5 0
0 10
0 0
15 4
0 0
16 8
6 1
2 11
0 0
0 0
17 7
9 12
0 0
0 0
0 18
0 0
3 0
14 0

样例输出2

13

---

样例 3, 4 有误, 请以 vijos 版本为准
(std出锅了...)

样例输入 3

见 bst3.in

样例输出 3

1845

该样例满足性质：\(r_i=0\)，\(1\le n\le 2000\)

样例输入 4

见 bst4.in

样例输出 4

185862

数据范围与约定

测试点编号	约定	测试点分值
1~4	\(1\le n\le 10\) , 且最多只需要进行一次修改，就可以成为二叉排序树	每个测试点5分
5~7	\(1\le n\le 20\)	每个测试点5分
8~10	\(1\le n\le 30\)	每个测试点5分
11~13	\(r_i=0\)，\(1\le n\le 2000\)	每个测试点5分
14~16	\(1\le n\le 2000\)	每个测试点5分
17~20	无特殊约定	每个测试点5分

对于所有的测试点，\(1\le n\le 2\times 10^5\) ，\(1\le a_i\le n\)