Limits

时间限制：1000ms

内存限制：128MB

Background

小M是G国的看守政府总理。12月2日晚，小M的离职仪式将在G国首都B市举行。

Description

离职仪式的现场可以描述为一个无限大的棋盘格平面，若干格内站着吹奏人员。为了美观起见，吹奏人员不会 相邻 站立。当某个吹奏人员的音量为\(v\)时，则其周围\((2v+1)×(2v+1)\)的范围的格子内都能听到音乐声。现在，小M要从她当前所在的格子走到出口所在的格子。每一步她都可以走到 相邻 的格子上，但她不能走到有吹奏人员的位置上。假定所有吹奏人员的音量相同，均为\(k\)。试问，当\(k\)为多少时，存在一条路径，使得小M在走向出口的过程中一直能听到音乐？求出\(k\)的最小值。

注意，“ 相邻 ”的格子意味着中心格子 周围的8个格子。

Input

第1行，仅一个整数\(n\)，表示吹奏人员的数量。

第2行，四个整数\(c_M,r_M,c_E,r_E\)，分别表示小M的初始格子的列号与行号（均从1开始计数）和出口的列号与行号。

接下来的\(n\)行，每行2个数\(c_i,r_i\)，表示每个吹奏人员的列号与行号。

Output

仅一个数，表示\(k\)的最小值。

Samples

Sample Input

3
3 6 7 1
4 5
5 3
7 2

Sample Output

1

Explanation

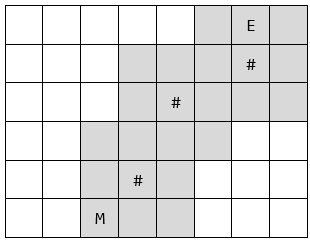
如图，灰色格子表示\(k=1\)时可以听到音乐的位置，“#”表示吹奏人员，“E”表示出口，而“M”小M的初始位置（这两处也可以听到音乐）。显然，\(k=1\)是最优解。

注意，若小M的初始位置和出口位置听不到音乐，则不是可行的方案。

Data range

对于30%的数据：\(1≤n≤10,-10^3≤c_i ,r_i,c_E,r_E,c_M,r_M≤10^3\)

对于60%的数据：\(1≤n≤100,-5×10^8≤c_i ,r_i,c_E,r_E,c_M,r_M≤5×10^8\)

对于100%的数据：\(1≤n≤1000,-5×10^{17}≤c_i ,r_i,c_E,r_E,c_M,r_M≤5×10^{17}\)