该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

Problem 2E. 子树最大值查询

题目描述

现有一棵 $n$ 点的树，每个结点有一个权值 $w_i$，初始情况下根为 $1$。

定义：结点的 价值 是该结点子树中，权值最大的结点的 权值。

回答 $q$ 次询问，每次询问给出 $u,v$，请输出：

• 若树以 $u$ 为根，则 $v$ 的 价值 是多少？

输入格式

第一行两个整数 $n, q$，表示树的结点数和询问次数。

接下来一行 $n$ 个整数，表示结点 $i$ 的权值。

接下来 $n - 1$​ 行每行两个整数，表示树的一条边。

接下来 $q$ 行每行两个整数 $u, v$，表示一次询问。

输出格式

对于每次询问输出一行表示答案。

样例输入1

6 4
1 2 3 4 5 6
1 3
1 6
2 6
3 4
3 5
4 1
6 3
2 4
4 4

样例输出1

6
5
4
6

样例1解释

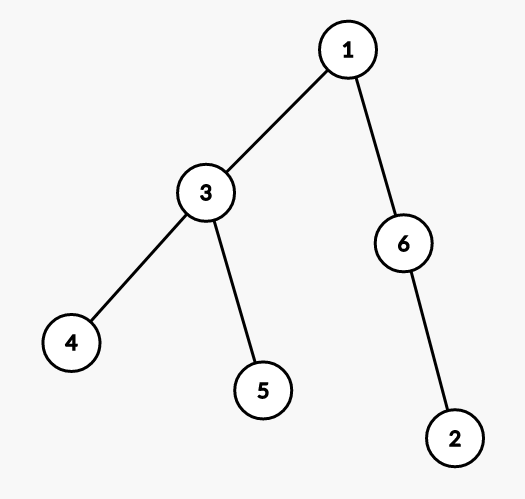
对于第一组询问，$3$ 的子树中结点的 权值 分别是 $3,1,6,2$，所以最大权值为 $6$​。

对于第三组询问，$4$ 的子树中结点的 权值 是 $4$，最大权值为 $4$。

注意到该样例为了演示，各结点的权值等于编号，其他测试点可能不满足这一点。

数据范围及限制

对于 $60\%$ 的数据，$1\le n,q\le 10^3$。

对于 $100\%$ 的数据，$1\le n,q\le 5\times 10^5, 1\le w_i\le n,1\le u,v\le n$。