该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

Problem 4D. 完全k叉树

时间限制：1s​

空间限制：16MB​

题目描述

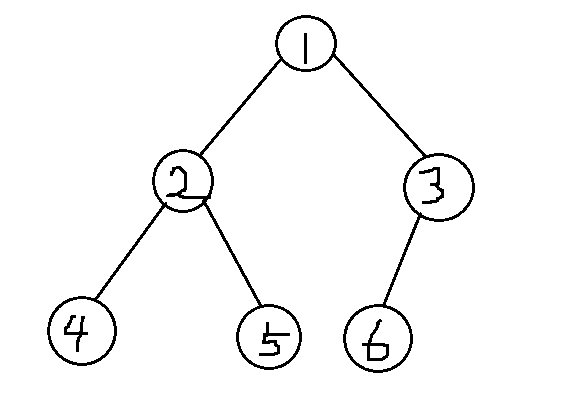
\(lhy\)在上数据结构的课上了解到，完全二叉树有顺序存储的方式。假设有这样的一棵完全二叉树：

我们可以存储为\(tree=[1,2,3,4,5,6]\)，它的含义是这样的：\(tree[0]\)是根结点；\(tree[i]\)的子结点是\(tree[2*i+1]\)和\(tree[2*i+2]\)。

看到这里，\(lhy\)就在想，完全\(k\)叉树是不是也可以这样存储呢。具体地，\(lhy\)准备这么存储一颗完全\(k\)叉树：\(tree[0]\)是树的根结点，\(tree[i]\)的子结点是\(tree[k*i+1],...,tree[k*i+k]\)。经过研究，\(lhy\)发现这么存储完全\(k\)叉树是不会发生冲突的，也可以很有效的利用空间，求子结点的效率也非常好。但是\(lhy\)觉得这样存储，求父结点的效率就差强人意了，因为给定了一个结点\(tree[i]\)，想要求它的父结点，就需要从根节点开始遍历，直到找到一个结点\(tree[ans]\)，它拥有子结点\(tree[i]\)，那么就可以说明\(tree[i]\)的父结点是\(tree[ans]\)，这样的做法往往就要遍历整颗树，性能极差。在这种情况下，\(lhy\)向你寻求帮助，希望你可以给出一个效率极高的算法。

具体来说，对于一颗完全\(k\)叉树，已知某个结点\(tree[i]\)存储在数组下标\(i\)的位置，询问它的父节点\(tree[ans]\)对应的下标\(ans\).

测试用例有多组。

数据格式

输入

第一行，一个正整数\(T\)表示测试用例的数量。

每个测试用例一行，两个正整数\(k,i\)，表示完全\(k\)叉树，结点\(tree[i]\)存储的位置。

输出

每个测试用例一行，一个正整数\(ans\)，表示\(tree[i]\)的父结点的位置。

样例

输入

5
2 1
3 10
2 4
1000000007 998244353
666 2333

输出

0
3
1
0
3

数据范围及约定

\(T \le 10^6, 2\le k \le 10^9, 1 \le i \le 10^9\).