该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

Problem 3E. 城市地铁旅行

时间限制：1s

空间限制：64MB

题目背景

$Mrj$ 市是一个美丽的旅游城市，拥有很多美丽的景区。

$Mrj$ 市旅游部为方便市民和游客在景点间旅行，兴修大量地铁线。并且为了节省经费，要求： 每个景区有且仅有一条从该景区出发的单向地铁线。

酷爱旅行的 $tsingpig$ 将乘坐出租车到达某个景区，在游览完该景区后乘坐地铁，前往其他景区。她拿到了$Mrj$ 市的地铁线路布局规划图，她希望知道从任意一个景区出发，乘坐地铁能够游览的最多景区数量。

题目描述

已知$Mrj$ 市拥有 $n$ 个旅游景区。

给定$Mrj$ 地铁线路规划图 $map[n]$ ，其中$map[i]$ 表示从景区 $i$ 出发的单向地铁线通往景区 $map[i]$, 并且保证其合法性（即$map[i] \in [0,n-1]$）。

请你帮助 $tsingpig$ 求解从每个景区出发、乘坐地铁进行城市旅行能够游览的 最大不重复 景区数量（包括出发景区）。

例如下图是一个$Mrj$ 市可能的地铁线路规划图。

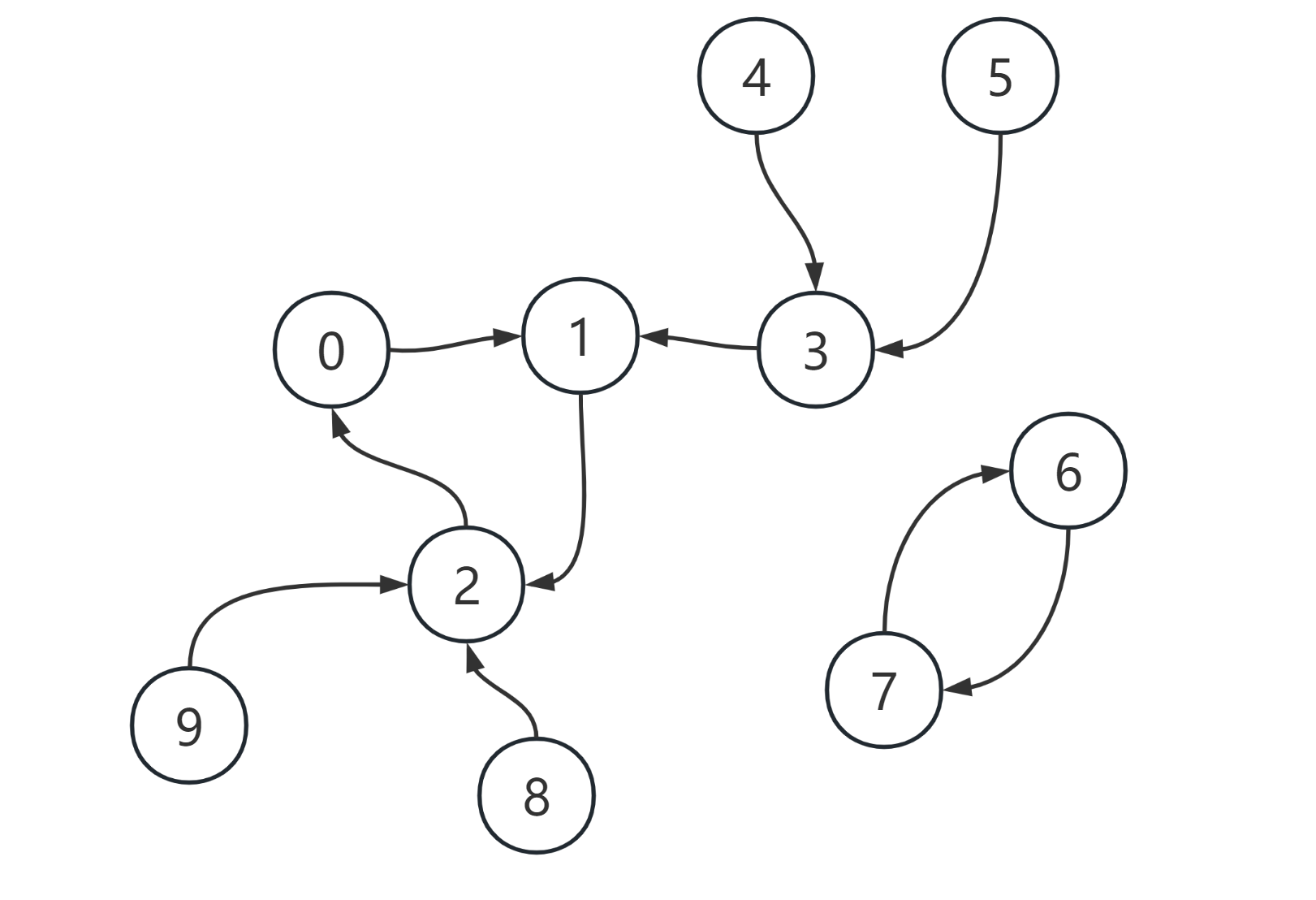
请注意：

• 首先，可以很明显的发现，地铁规划图一定有且仅有 $n$ 条地铁线路。
• 其次，规划图是允许 $map[i] == i$ 的。你可以看成没有从该景区 出发 的地铁线，也可以理解为该景区有一条从自己出发回到自己的环。
• 另外，地铁规划图是一个有向图，其对应的无向图未必是连通的。你可以认为每一个连通分量是$Mrj$ 市的一个独立区，它的地铁线路和其他区域显然没有连接。
• 最后，请你计算的结果中不要重复计算相同的景区，也就是说 $tsingpig$ 不希望重复游览相同的景区。

输入格式

• 第一行正整数$n$，表示城市有$n$ 个旅游景区。
• 第二行$n$ 个数，构成地铁线路规划图 $map[n]$ ，其中$map[i]$ 表示从景区 $i$ 出发的地铁线通往景区 $map[i]$, 并且保证其合法性（即$map[i] \in [0,n-1]$）

输出格式

输出$n$ 个数，第 $i$ 个数表示 从 $i$ 景区出发，能够游览的 最大不重复 景区数量（包括出发景区）。

样例输入 1

5
1 2 3 4 0

样例输出 1

5 5 5 5 5

样例输入 2

5
1 2 0 0 4

样例输出 2

3 3 3 4 1

解释：对于景区4，只有一条从自己出发回到自己的地铁线（或者理解成没有修建从景区4出发的地铁线），所以游览的景区数量是1

样例输入 3

75
1 38 45 3 5 63 69 13 22 15 14 28 49 74 25 12 18 36 62 53 40 7 17 60 41 61 68 73 39 67 65 8 72 48 64 43 57 19 32 55 51 9 20 47 10 6 35 16 31 30 21 70 29 37 23 71 27 33 52 56 11 24 54 26 0 34 2 42 50 59 4 58 66 46 44 

样例输出 3

63 63 63 1 63 63 63 63 8 63 63 63 63 63 63 63 63 8 63 3 63 63 8 63 63 63 63 63 63 63 63 8 63 8 63 63 8 3 63 63 63 63 63 63 63 63 63 63 8 63 63 63 63 3 63 63 63 8 63 63 63 63 63 63 63 63 63 63 63 63 63 63 63 63 63 

数据范围及限制

对于60%的数据，$n \in [1,1000]$

对于100%的数据，$n \in [1,10^6]$