基本思想——折半

二分法的基本思想比较简单，是用来在数组当中查找特定元素的算法。

二分可以分为整数二分和浮点二分，本文主要介绍整数二分。

具体步骤

首先，从数组的中间元素开始搜索，如果该元素恰好是目标元素，则搜索过程结束，否则继续执行。
如果目标元素大于/小于中间元素，则在数组大于/小于中间元素的那一半区域查找，然后重复上一步的操作。

如果某一步数组为空，则表示找不到目标元素。

边界更新的两种方式

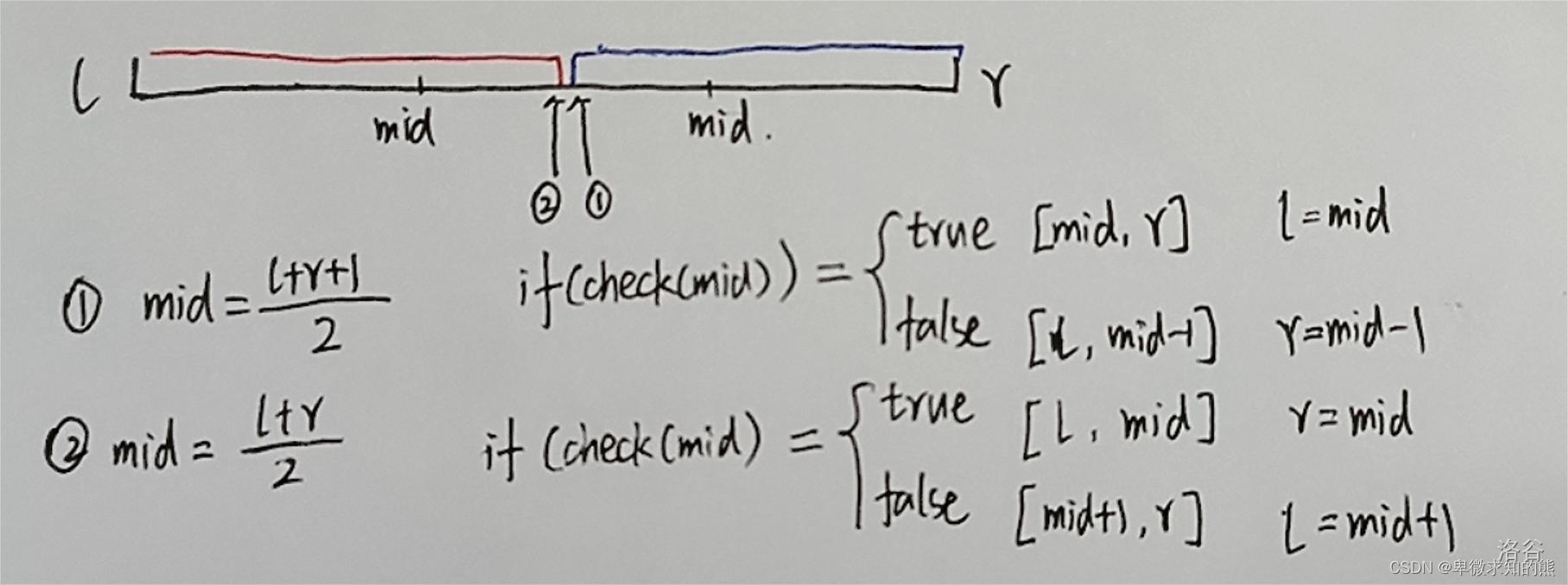
1. 当 mid=l+r+1>>1 时，查找值指向箭头2位置，检查 mid 是否满足红色部分性质，如果成立的话，mid 便在红色区域当中，此时，查找值便在区域 [mid，r] 里面，此时更新边界的方法为 l=mid 。如果不成立的话，mid 便在蓝色区域当中，此时查找值便在区域 [l，mid-1] 里面，此时更新边界的方法为 r=mid-1 。

2. 当 mid=l+r>>1 时，查找值指向箭头1位置，检查 mid 是否满足蓝色部分性质，如果成立的话，mid 便在蓝色区域当中，此时，查找值便在区域 [l，mid] 里面，这里要注意包含边界，因为我们的查找值可能就是边界，此时更新边界的方法为 r=mid 。如果不成立的话，mid 便在红色区域当中，此时查找值便在区域 [mid，r] 里面，此时更新边界的方法为 l=mid+1 。

注意事项

二分法特别需要注意左右两端的边界问题，如果发生问题绝大部分都是由边界产生的，因此本文提供三种模板来应对不同情况下的二分问题。

单调性与二分法并没有直接关系。如果题目具有单调性的话我一定可以使用二分法，但是我可以使用二分法的题目不一定非得由单调性。

C++ 整数除法是 向下取整。

来源

2023-7-11 09:35:08
创建人 root