出动
背景
Gallifrey的时间领主终于卷土重来,时间领主组织了一支先锋队前往斯卡洛星球对抗戴立克军团。孤立于Gallifrey和斯卡洛星球的时间领主军团很快就遭到了戴立克军团的重重包围,现在他们将主力只好聚集了起来,以抵抗戴立克军团的围剿。可怕的是,他们之中有人感染上了戴立克最新科技:纳米云,它可以让时间领主转化为戴立克,如果不设法阻止纳米云的扩散,很快就会遭到灭顶之灾。时间领主总统拉西隆已经开始调查纳米云的源头,发现那是戴沃斯发明的。你是在你戴沃斯转化的人形戴立克。戴沃斯希望这样快速地攻破时间领主的防御,打败这个生存于三维世界却突破了时间维度的种族。
描述
军团是一个 \(n\) 行 \(m\) 列的矩阵,每个单元是一个时间领主军团的成员。感染纳米云的人,每过一个小时,就会向四周扩散纳米云,直到所有人全部转化为戴立克。你已经掌握了感染源的位置,任务是算出时间领主们感染纳米云的时间,并且将它报告给戴沃斯,以便对时间领主们进行一轮有针对性的围剿。
格式
输入格式
第 \(1\) 行:四个整数 \(n\),\(m\),\(a\),\(b\),表示军团矩阵有 \(n\) 行 \(m\) 列。有 \(a\) 个感染源,\(b\) 为时间领主们的数量。
接下来 \(a\) 行:每行有两个整数 \(x\),\(y\),表示感染源在第 \(x\) 行第 \(y\) 列。
接下来 \(b\) 行:每行有两个整数 \(x\),\(y\),表示领主的位置在第 \(x\) 行第 \(y\) 列。
输出格式
第 \(1\) 至 \(b\) 行:每行一个整数,表示这个时间领主感染纳米云的时间,输出顺序与输入顺序一致。如果某个人的位置在感染源,那么他感染纳米云的时间为 \(0\)。
样例1
输入样例1
5 4 2 3
1 1
5 4
3 3
5 3
2 4
输出样例1
3
1
3
样例解释
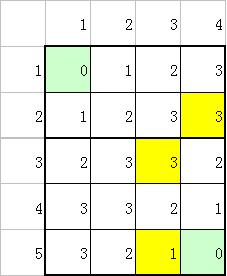
如下图,标记出了所有人感染纳米云的时间以及感染源和时间领主的位置。
限制
对于 \(100\%\) 的数据,保证 \(1\le n,m\le500\),\(1\le a,b\le10^5\)。