题目描述

给定平面上 \(n\) 个不同的点，每两个点连接一条直线，连接的直线如果重合算是一条直线，请编程求有多少对（一对是指两条）直线相交，可参考样例理解。

格式

输入格式

第一行包含一个整数 \(n\)，表示平面中不同点的个数。

接下来 \(n\) 行，每行包含 \(2\) 个整数 \(x_i,y_i\)，表示给出的第 \(i\) 个点的坐标。

输出格式

输出仅一行包含一个整数 \(m\)，表示平面内有 \(m\) 对直线相交。

样例1

样例输入1

4
0 0
0 2
0 4
2 0

样例输出1

6

样例2

样例输入2

3
-1 -1
1 0
3 1

样例输出2

0

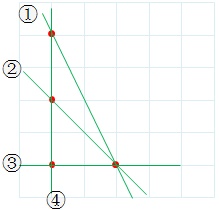
样例1解释

相交的 \(6\) 对直线分别是 \(\{①④\},\{②④\},\{③④\},\{①②\},\{①③\},\{②③\}\)

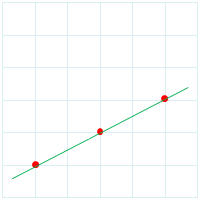
样例2解释

如下图，三个点在同一条直线上。

限制

\(40\%\)的数据：\(n ≤ 100\)；

\(100\%\)的数据：\(2 ≤ n ≤ 1000, -10^4 ≤ x_i,y_i ≤ 10^4\)。