题目描述

Smart 的第一片矿区已经开始运作了，他着手开展第二片矿区……

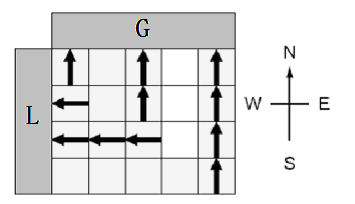
Smart 的第二片矿区里面有全宇宙最稀有的两种矿物，科学家称其为 \(G\) 矿和 \(L\) 矿。 矿区是被划分成一个 \(n×m\) 的矩形区域。Smart 探明了每一小块区域里的 \(G\) 矿和 \(L\) 矿的蕴藏量，并且 Smart 还在矿区的北边和西边分别设置了 \(G\) 矿和 \(L\) 矿的收集站。你的任务是设计一个管道运输系统，使得运送的 \(G\) 矿和 \(L\) 矿的总量最多。

管道的型号有两种，一种是东西向，一种是南北向。在一个格子内你能建造一种管道，但不能两种都建。如果两个同类型管道首位相接，它们就可以被连接起来。

另外这些矿物都十分不稳定，因此它们在运送过程中都不能拐弯。这就意味着如果某个格子上建有南北向管道，但是它北边的格子建有东西向管道，那么这根南北向管道内运送的任何东西都将丢失。进一步地，运到 \(G\) 矿收集站的 \(L\) 矿也会丢失，运到 \(L\) 矿收集站的 \(G\) 矿也会丢失。

格式

输入格式

第一行包含两个整数 \(n\) 和 \(m\)，表示矿区大小。

以下 \(n\) 行，每行 \(m\) 个整数，其中第 \(i\) 行第 \(j\) 个整数\(L[i][j]\)描述各个格子上的 \(L\) 矿数量。接下来以类似的矩阵表示各个格子上的 \(G\) 矿数量。

输出格式

仅一个整数，表示最多可以采集到的 \(G\) 矿和 \(L\) 矿的总量。

样例1

样例输入1

4 4
0 0 10 9
1 3 10 0
4 2 1 3
1 1 20 0
10 0 0 0
1 1 1 30
0 0 5 5
5 10 10 10

样例输出1

98

样例2

样例输入2

2 9
497 681 843 822 133 286 780 670 218 
116 45 740 378 626 654 566 362 342 
311 549 95 117 685 723 15 110 468 
778 766 218 581 830 946 590 403 174 

样例输出2

9066

限制

\(30\%\)的数据：\(0≤n，m≤100\)；

\(100\%\)的数据：\(0≤n, m≤1000，0≤L[i][j]，G[i][j]≤1000\)。