题目描述

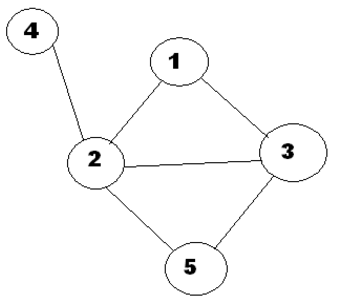
FJ 的农场有 \(n\) 个牛舍，这些牛舍通过 \(m\) 条道路连接在一起，奶牛贝蒂可以从任何一个牛舍出发，然后通过连通的道路经过两个不同的牛舍后到达目标牛舍，（注意目标牛舍也可能就是出发的那个牛舍），例如下图，贝蒂可以从走 \(1 -> 2 -> 3 -> 5\)，也可以走 \(1 -> 2 -> 3 -> 1\) ，这都是合法的，但不能走 \(1 -> 2 -> 1 -> 2\) 或者 \(1 -> 2 -> 3 -> 2\)，这都是非法的，也就是说中间经过的牛舍不能和起点或终点相同。那么现在请你帮贝蒂算一下，贝蒂的旅行方案总共有多少种。数值可能很大，请对 \(100000007\) 取模。

格式

输入格式

输入第 \(1\) 行两个整数 \(n\) 和 \(m\)，含义如题意描述。

接下来 \(m\) 行，每行两个整数，表示两个相连的牛舍门牌号。

输出格式

输出一行一个整数，表示贝蒂的旅行方案总数。

样例1

样例输入1

3 3
1 2
2 3
1 3

样例输出1

6

样例解释

总共 \(6\)种旅行方案：

\(1 -> 2 -> 3 -> 1\)

\(1 -> 3 -> 2 -> 1\)

\(2 -> 1 -> 3 -> 2\)

\(2 -> 3 -> 1 -> 2\)

\(3 -> 2 -> 1 -> 3\)

\(3 -> 1 -> 2 -> 3\)

限制

对于 \(100\%\) 的数据，\(1<=n<=10000, 1<=m<=100000\)

来源

地址：\(\text{Online~Judge}\)
作者：\(hoogy\)
模拟赛\(T3\)