题目描述

丽江河边有 \(n\) 家很有特色的客栈，客栈按照其位置顺序从 \(1\) 到 \(n\) 编号。每家客栈都按照某一种色调进行装饰（总共 \(k\) 种，用整数 \(0 \sim k-1\) 表示），且每家客栈都设有一家咖啡店，每家咖啡店均有各自的最低消费。

两位游客一起去丽江旅游，他们喜欢相同的色调，又想尝试两个不同的客栈，因此决定分别住在色调相同的两家客栈中。晚上，他们打算选择一家咖啡店喝咖啡，要求咖啡店位于两人住的两家客栈之间（包括他们住的客栈），且咖啡店的最低消费不超过 \(p\) 。

他们想知道总共有多少种选择住宿的方案，保证晚上可以找到一家最低消费不超过 \(p\) 元的咖啡店小聚。

格式

输入格式

共 \(n+1\) 行。

第一行三个整数 \(n, k, p\)，每两个整数之间用一个空格隔开，分别表示客栈的个数，色调的数目和能接受的最低消费的最高值；

接下来的 \(n\) 行，第 \(i+1\) 行两个整数，之间用一个空格隔开，分别表示 \(i \) 号客栈的装饰色调 \(a_i\) 和 \(i\) 号客栈的咖啡店的最低消费 \(b_i\)。

输出格式

一个整数，表示可选的住宿方案的总数。

样例1

样例输入1

5 2 3 
0 5 
1 3 
0 2 
1 4 
1 5

样例输出1

3

样例解释

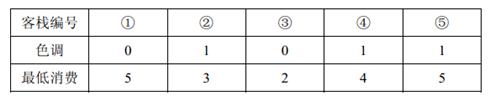
\(2\) 人要住同样色调的客栈，所有可选的住宿方案包括：住客栈 \(①③，②④，②⑤，④⑤\)，但是若选择住 \(4,5\)号客栈的话，\(4,5\) 号客栈之间的咖啡店的最低消费是 \(4\) ，而两人能承受的最低消费是 \(3\) 元，所以不满足要求。因此只有前 \(3\) 种方案可选。

限制

• 对于 \(100\%\) 的数据，有 \(2 \leq n \leq 2 \times 10^5\)，\(1 \leq k \leq 50\)，\(0 \leq p \leq 100\)，\(0 \leq b_i \leq 100\)。