题目描述

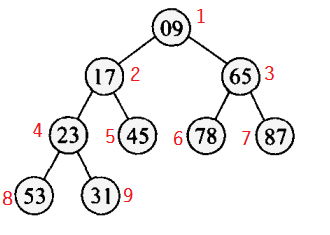
堆是一棵完全二叉树，就像下面这棵树一样。

上图的这棵完全二叉树有一个特点，就是所有父结点的权值都比子结点的权值要小（注意：圆圈里面的数是权值，圆圈上面的数是这个结点的编号）。符合这样特点的完全二叉树我们称为小根堆。

小根堆的根的权值最小，且根的两个子树也是一个小根堆。可以用一个数组\(a[\ ]\)来记录一棵完全二叉树，\(a[1]\)为根结点，若结点\(a[i]\)不是根结点，那么它的父亲为\(a[i/2]\)（取下整）；若结点\(a[j]\)不是叶子结点，那么它的左儿子为\(a[2×j]\)，它的右儿子为\(a[2×j+1]\)。

现在给你一列\(n\)个数，要你按一定顺序依次插入数组\(a[\ ]\)中（即第\(i\)个数为\(a[i]\)），这个数组\(a[\ ]\)记录的完全二叉树最后得出来的就已经是一个小根堆，若有多种方法，输出字典序最大的一组。

格式

输入格式

第\(1\)行为一个正整数\(n\)，表示数列的长度。

第\(2\)行包含\(n\)个正整数，为这个数列的\(n\)个数，数字之间用空格隔开。

输出格式

输出一行\(n\)个数，依次输出描述小根堆的完全二叉树的数组\(a\)，数字之间用空格隔开，行末换行并没有空格。

样例1

样例输入1

3
1 2 3

样例输出1

1 3 2

样例解释

1 2 3 与 1 3 2 都是满足要求，但是 1 3 2 的字典序更大。

限制

测试点编号	\(x\)
\(1,2,3\)	\(n≤15\)
\(4,5\)	\(n≤1023\)
\(6,7,8,9,10\)	\(n≤65535\), 所有数字不超过 \(10^8\)