题目描述

设有一棵二叉树，如图：

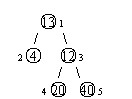
其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 \(1\)。

如上图中，若医院建在 \(1\) 处，则距离和为：
\[4+12+2\times20+2\times40=136\]

若医院建在 \(3\) 处，则距离和为：
\[4\times2+13+20+40=81\]

格式

输入格式

第一行一个整数 \(n\)，表示树的结点数。

接下来的 \(n\) 行每行描述了一个结点的状况，包含三个整数 \(w, u, v\)，其中 \(w\) 为居民人口数，\(u\) 为左链接（为 \(0\) 表示无链接），\(v\) 为右链接（为 \(0\) 表示无链接）。

输出格式

一个整数，表示最小距离和。

样例1

样例输入1

5                       
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

样例输出1

81

限制

对于 \(100\%\) 的数据，保证 \(1 \leq n \leq 100\)，\(0 \leq u, v \leq n\)，\(1 \leq w \leq 10^5\)。