题目描述

给你一棵 \(n\) 个顶点的树（即无向无环连通图）。 树中的 \(n-1\) 条边，每条边都用黑色或红色着色。

给定你一个整数 \(k\)，考虑 \(k\) 个顶点的序列，如果满足以下条件，就称顶点序列 \([a_1, a_2, …, a_k]\)其为前卫序列：

\(1.\) 从顶点 \(a_1\) 到 \(a_k\) 存在一条路径可走（可能多次访问相同的边或顶点）。

\(2.\) 从顶点 \(a_1\) 开始，然后走 \(a_1\) 和 \(a_2\) 之间的最短路径进入 \(a_2\)，然后以类似的方式进入 \(a_3\)，依此类推，直到经过 \(a_{k-1}\) 和 \(a_k\) 之间的最短路径。

\(3.\) 在此过程中走过了至少一个黑色边。

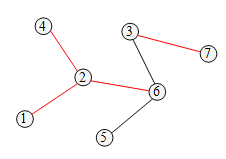
例如，在下图中树，如果 \(k=3\)，则顶点序列 \([1, 4, 7]\)，\([5, 5, 3]\) 和 \([2, 3, 7]\) 都是前卫序列（不止这些），而顶点序列 \([1, 4, 6]\)，\([5, 5, 5]\) 和 \([3, 7, 3]\) 则不是前卫序列。

易知长度为 \(k\) 的顶点序列共有 \(n^k\) 个，计算其中有多少个顶点序列是前卫的。由于此数字可能很大，请模 \(10^9 + 7\) 后输出。

格式

输入格式

第一行包含两个整数 \(n\) 和 \(k\)，表示树的大小和顶点序列的长度。

接下来的 \(n-1\) 行中的每行包含三个整数 \(u,v\) 和 \(x\)，其中顶点 \(u\) 和 \(v\) 之间有一条边，这条边的颜色为 \(x\)（\(x=0\)表示红色，\(1\)表示黑色）。

输出格式

输出一行一个整数，答案对 \(10^9+7\) 取模。

样例1

输入样例1

4 4
1 2 1
2 3 1
3 4 1

输出样例1

252

样例解释

顶点序列总数为\(4^4=256\)，下面的\(4\)个顶点序列不满足要求，分别是\([1, 1, 1, 1]\)、\([2, 2, 2, 2]\)、\([3, 3, 3, 3]\)、\([4, 4, 4, 4]\)，所以前卫序列共有\(252\)个。

限制

\(100\%\)的数据：\(2\le n \le 10^5，2 \le k \le 100\)。