题目描述

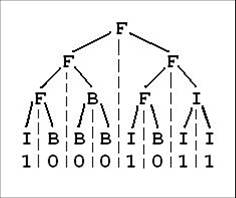
我们可以把由“\(0\)”和“\(1\)”组成的字符串分为三类：全“\(0\)”串称为\(B\)串，全“\(1\)”串称为I串，既含“\(0\)”又含“\(1\)”的串则称为F串。\(FBI\)树是一种二叉树。

( 二叉树：二叉树是结点的有限集合，这个集合或为空集，或由一个根结点和两棵不相交的二叉树组成。这两棵不相交的二叉树分别称为这个根结点的左子树和右子树。)

它的结点类型也包括\(F\)结点，\(B\)结点和\(I\)结点三种。由一个长度为\(2^N\)的“\(01\)”串S可以构造出一棵\(FBI\)树\(T\)，递归的构造方法如下：

1. \(T\)的根结点为\(R\)，其类型与串\(S\)的类型相同；
2. 若串\(S\)的长度大于\(1\)，将串\(S\)从中间分开，分为等长的左右子串\(S_1\)和\(S_2\)；由左子串\(S_1\)构造R的左子树\(T_1\)，由右子串\(S_2\)构造\(R\)的右子树\(T_2\)。

现在给定一个长度为\(2^N\)的“\(01\)”串，请用上述构造方法构造出一棵\(FBI\)树，并输出它的后序遍历序列。

(后序遍历：后序遍历是深度优先遍历二叉树的一种方法，它的递归定义是：先后序遍历左子树，再后序遍历右子树，最后访问根。)

格式

输入格式

第一行是一个整数\(N(0 \le N \le 10)\)，

第二行是一个长度为\(2^N\)的“\(01\)”串。

输出格式

一个字符串，即\(FBI\)树的后序遍历序列。

样例1

样例输入1

3
10001011

样例输出1

IBFBBBFIBFIIIFF

限制

对于\(40\%\)的数据，\(N \le 2\)；

对于全部的数据，\(N \le 10\)。