题目描述

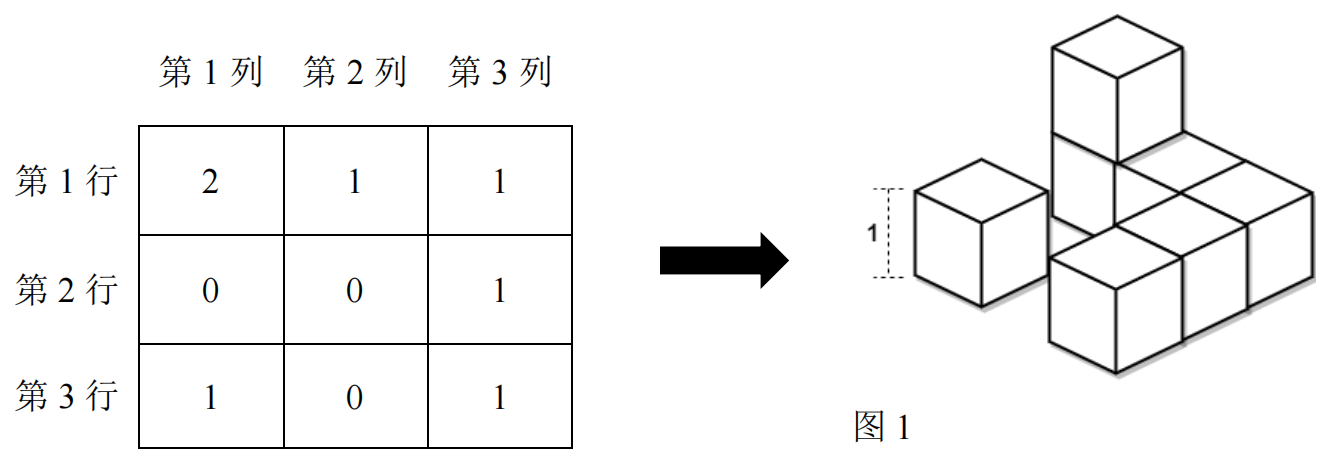
在 \(n\) 行 \(n\) 列\(（n≤50）\)的正方形网格上，整齐的叠放着一些长、宽、高都为 \(1\) 的正方体。输入数据逐行逐列提供了每个单元格里叠放的正方体个数 \(h（h≤50）\)。如图 \(1\) 所示，在一个\(3\) 行 \(3\) 列的正方形网格上，叠放着 \(7\) 个正方体，其表面积为 \(32\)。

所有正方体放好后，相互接触的正方体会粘贴在一起，形成不规则的三维物体，请计算出物体的表面积。
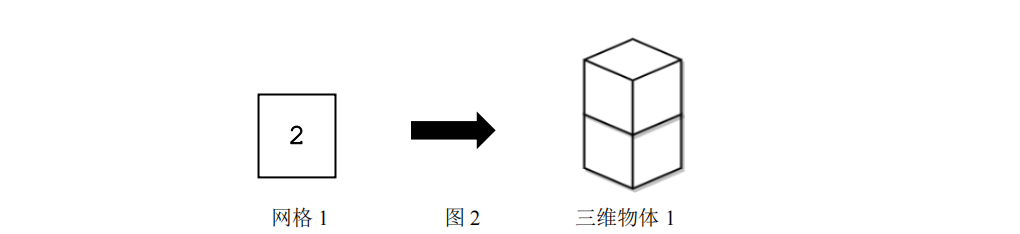
如图 \(2\) 所示，在 \(1\) 行 \(1\) 列的网格 \(1\) 内，叠放了 \(2\) 个正方体。对应的三维物体 \(1\) 的表面积为 \(10\)。

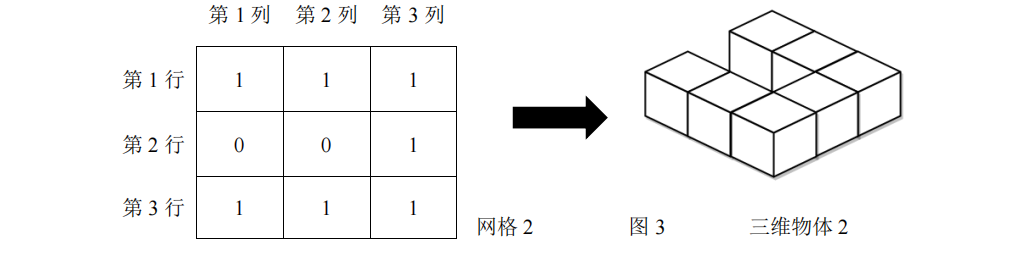
如图 \(3\) 所示，在 \(3\) 行 \(3\) 列的网格中，每个单元格内叠放的正方体数量见网格 \(2\)。对应的三维物体 \(2\) 的表面积为 \(30\)。

格式

输入格式

第一行一个正整数\(n\)。

接下来一个矩阵\(a_i\)，意义见上。

输出格式

即三维物体的表面积。

样例1

输入样例1

3
2 1 1
0 0 1
1 0 1

输出样例1

32

提示

思路1

按照输入数据的次序枚举所有单元格。假设某单元格里叠放了 \(h\) 个正方体，若 \(h>0\)，则 其顶部、底部对物体表面积的贡献都是 \(1\)。但由于受到相邻单元格的影响，其前后左右四个侧面对物体表面积的贡献则不一定是 \(h\)。方法一的思路就是在枚举的过程中，统计每个单元格的顶部、底部、前后左右四个侧面，共六个面对表面积的贡献。最后得出表面积的大小。

思路2

按照输入数据的次序枚举所有单元格，先直接算出全部正方体的表面积。若网格中共有 \(m\) 个立方体，每个立方体有六个面，则表面积是\(6 × m\)。但是直接相邻的正方体会粘贴在一 起，它们之间产生的接触面会让表面积减少 \(2\)。假设全部正方体之间共有个接触面，最终表面积就是\(6 × m − 2 × e\) 。那么如何在枚举的过程中统计出立方体之间有多少个接触面呢？