线段树的基本应用

一.扫描线

\(1.1\) 引入

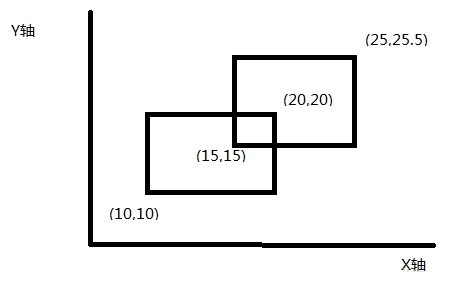
有时候我们求一个给定的平面直角坐标系中的 \(N\) 个矩形的面积，而此时，我们就需要引入一种高效且奇妙的算法——扫描线。
例如该图：

\(1.2\) 分析

我们将其中的矩形按上下边，构建 \(4\) 条扫描线，并按照 \(Y\) 值大小进行排序，并标记为上或下。 但是由于矩形的 \(X\) 坐标有 \(4\) 个，并且相互关联，而想要提升算法效率就必须尽可能规避大的状态转移（区间，信息合并），所以我们将 \(x\) 节点离散化，此时，我们就可以用类似线段树来维护信息。

\(\text{PS}\):离散化：进行区间映射，并删除重复（主要用来减少空间大小）

此时，我们用 \(4\) 个不同的 \(x\) 坐标把 \(x\) 轴分成了 \(3\) 段有效的区间.这里要注意我们线段树中每个叶节点控制的是区间 \([X[L],X[L+1]]\).线段树中其他节点控制的区间 \([L,R]\),也是指的 \(x\) 坐标轴的第 \(L\) 个区间到第 \(R\) 个区间的范围,也就是 \(X[L]\) 到 \(X[R+1]\) 坐标的范围。

考虑如何用此时有效的信息进行最后答案的求值：

\(1.\) 以 \(Y\) 坐标从小到大的顺序读入每条扫描线
\(2.\) 记录当前所读入的所有扫描线能有效覆盖 \(X\) 轴的最大长度 \(sum[1]\).
\(3.\) 用 \(mark[i]\) 记录线段树中第 \(i\) 个节点是否被完全覆盖，以及完全覆盖次数，当为下位边 \(+1\)，上位边 \(-1\)。

建议自己进行模拟，感受一下长度的加减与边上下的关系，同时感受 \(mark\) 的妙用。

\(1.3\) 代码实现

建立结构体：（详情看注释） 按节点存储信息

//以横坐标作为线段(区间),对横坐标线段进行扫描
//扫描的作用是每次更新下底边总长度和下底边个数,增加新面积 
struct node{//线段 
    double l,r,h;
    int d;
    //l: 表示扫描线的左端x坐标
    //r:表示扫描线的右端x坐标
    //h: 表示扫描线的高度
    //d: 为1或-1,标记扫描线是矩形的上位还是下位边.
    node(){}
    //结构体初始化
    node(double x1,double x2,double H,int c):l(x1),r(x2),h(H),d(c){}
    //重载运算（相当于cmp）
    bool operator<(const node &a)const{
        return h<a.h;
    }
}s[500005];

读入所有矩形的信息,更新扫描线,并且把矩形的两个端点 \(x\) 坐标放入 \(X\) 数组中,对 \(node\) 和 \(X\) 都排序,\(node\) 按 \(h\) 值从小到大排序. \(X\) 按从小到大排序.
对 \(X\) 数组去重,并且用 \(k\) 表示一共有多少个 \(X\).\(X[i]\) 和 \(X[i+1]\) 表示第 \(i\) 个区间长度.
函数以及变量含义：

\(mark\): \(>=0\) 时表示本节点控制的区域内下位边个数 \(-\) 上位边个数的结果.此时可以累加进 \(sum\) 中
\(sum\): 本节点控制的区域内 \(mark\) 值不为 \(0\)(大于 \(0\))的区域总长度.
线段树操作:

\(\text{PushUp(i,l,r)}\): 根据子节点的 \(mark\) 值和 \(sum\) 值更新父节点的 \(mark\) 和 \(sum\) 值,也就是更新自己，由于递归的原因，最终所有的更新都会回到根节点。

\(\text{update(ql,qr,d,i,l,r)}\): 使得 \([ql,qr]\) 与 \([l,r]\) 区间的公共部分 \(mark\) 值 \(+d\).
判断： ql<=l && r<=qr 且 \(mark[i]!=0\) 的话： 更新并 \(return\)

\(PS\):\(mark[i]\) 不存在 \(-1\) 的情况（如果遍历到了上位边且会使 \(mark[i]-1\)，那么一定在之前遍历到了相同的下位边使它 \(+1\)，最小为 \(0\) 的情况）
在一次递归更新左右儿子 最后信息上传（\(pushup\)).

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<queue>
#include<algorithm>
#include<map>
#include<iomanip>
#define INF 99999999
using namespace std;

//mark[i] 表示对于线段树第i个节点是否可以累加进sum，也就是下位边覆盖次数是否大于上位边
//sum[i]  表示对于线段树第i个节点可以成功累加的长度 
//X[i]    表示离散化之后的点编号（区间的端点） 
const int MAX=1000005;
int mark[MAX<<2];
long long sum[MAX<<2];
long long x[MAX];

//线段 
struct seg{
    long long l,r,h;
    int d;
    seg(){}
    seg(long long x1,long long x2,long long H,int c):l(x1),r(x2),h(H),d(c){}
    bool operator<(const seg &a)const{
        return h<a.h;
    }
}s[MAX];
 
void pushup(int n,int left,int right){
    if(mark[n])sum[n]=x[right+1]-x[left];
    else if(left == right)sum[n]=0;
    else sum[n]=sum[n<<1]+sum[n<<1|1];
}
 
void Update(int L,int R,int d,int n,int left,int right){
    //当当前区间被完全覆盖时，直接更新信息，结束 
    if(L<=left && right<=R){
        mark[n]+=d;
        pushup(n,left,right);
        return;
    }
    //没有被完全覆盖，向下递归，最后更新信息 
    int mid=left+right>>1;
    if(L<=mid)Update(L,R,d,n<<1,left,mid);
    if(R>mid)Update(L,R,d,n<<1|1,mid+1,right);
    pushup(n,left,right);
}

//二分查找，在已经更新的X中寻找当前扫描线左右端点的编号（应该是没有-1情况的......） 
int search(long long key,long long* x,int n){
    int left=0,right=n-1;
    while(left<=right){
        int mid=left+right>>1;
        if(x[mid] == key)return mid;
        if(x[mid]>key)right=mid-1;
        else left=mid+1;
    }
    return -1;
}
 
int main(){
    int n,num=0;
    long long x1,x2,y1,y2;
    cin>>n;
    int k=0;
    //读入矩形，构造扫描线，更新信息 
    for(int i=0;i<n;++i){
        cin>>x1>>y1>>x2>>y2;
        x[k]=x1;
        s[k++]=seg(x1,x2,y1,1);
        x[k]=x2;
            s[k++]=seg(x1,x2,y2,-1);
    }
    //离散化&去重 
    sort(x,x+k);
    sort(s,s+k);
    int m=1;
    for(int i=1;i<k;++i)
        if(x[i] != x[i-1])
            x[m++]=x[i];
    long long ans=0;
    //根据扫描线的左右端点更新答案 
    for(int i=0;i<k;++i){
        int L=search(s[i].l,x,m);
            int R=search(s[i].r,x,m)-1;
        Update(L,R,s[i].d,1,0,m-1);
        ans+=sum[1]*(s[i+1].h-s[i].h);
    }
    printf("%lld\n",ans);
    return 0;
}

• \(by\) \(jialiang2509\)