时间限制：1 S

内存限制：64 MB

【题目描述】

质数：是一个大于 $1$ 的自然数，且除了 $1$ 和它本身外，不能被其它自然数整除的数。最小的质数是 $2$ ，$1$ 不是质数。

合数：一个正整数，如果除 $1$ 和它本身以外，还能被其它正整数整除，叫合数。如 $6$ 是合数，除了 $1$ 和 $6$ 以外，还能被 $2$ 和 $3$ 整除。

分解质因数：每个合数都可以写成几个质数相乘的形式，其中每个质数都是这个合数的因数，把一个合数用质因数相乘的形式表示出来，叫做分解质因数（分解质因数只针对合数）。如合数 $12 = 2 × 2 × 3$ 。

分解质因数的方法是先用这个合数的最小质因数去除这个合数，结果若是一个质数就不再除下去；若是一个合数就继续按原来的方法从最小质因数除起，直至最后除得的结果是一个质数。

给定一个合数 $N$ ，将 $N$ 分解质因数后，输出其质因数个数。

【输入格式】

输入一个合数 $N$ ($N < 1000$) 。

【输出格式】

将 $N$ 分解质因数后，输出质因数个数。

样例 1

【样例 1 输入】

18

【样例 1 输出】

3

【样例 1 解释】

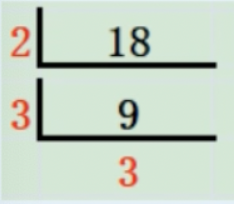
合数 $18$ 分解质因数，首先用最小质因数 $2$ 去除，除后结果为合数 $9$ ，继续用最小质因数 $3$ 去除，除后结果为质数 $3$ ，就不再除下去。所以 $18$ 的质因数为 $2$ , $3$ , $3$ ，故质因数的个数为 $3$ 。