时间限制：1 S

内存限制：64 MB

【题目描述】

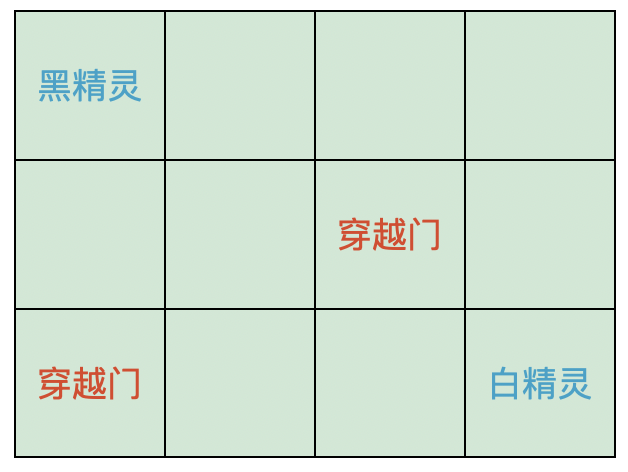
在一个矩阵精灵王国里有两个精灵，一个叫黑精灵，一个叫白精灵。他们住在一个 \(N \times M\) 的矩阵方格中的不同位置，黑精灵住在矩阵方格的左上角方格里 \((1 , 1)\) ，白精灵住在矩阵方格的右下角方格里 \((N , M)\) 。

在这个矩阵方格里还有一对可穿越的门，这对穿越门的位置不固定，位置可变换（穿越门不会出现在矩阵方格左上角和右下角位置，也不会重叠出现，有且只有一对）。穿越门的功能是当进入其中一扇门的位置后可直接穿越到另一扇门的位置。

如下图所示：

一天黑精灵要去白精灵家做客，需要穿过方格矩阵到达白精灵家，穿行矩阵方格要求：

1. 每次只能走一个方格，可以向上、向下、向左、向右行走；

2. 每走一个方格计为 \(1\) 步，但从一扇穿越门穿越到另一扇穿越门不计步数（从方格走到穿越门和从穿越门到其它方格都计 \(1\) 步）；

3. 可借助穿越门去白精灵家（可减少行走步数）。

为了尽快到达白精灵家，请你帮助黑精灵找一条最短路线，并且计算出最短路线的步数。

【输入格式】

第一行输入两个以一个空格隔开的正整数 \(N\) , \(M\) (\(2 < 𝑁 , 𝑀 < 101\))，分别表示 \(N\) 行 \(M\) 列的方格矩阵；

接下来第二行输入两个以一个空格隔开的正整数：\(N_1\) (\(N_1 ≤ N\)) , \(M_1\) (\(M_1 ≤ M\)) ，代表第一个穿越门位于第 \(N_1\) 行第 \(M_1\) 列；

接下来第三行输入两个以一个空格隔开的正整数：\(N_2\) (\(N_2 ≤ N\)) , \(M_2\) (\(M_2 ≤ M\)) ，代表第二个穿越门位于第 \(N_2\) 行第 \(M_2\) 列；

注意：两个穿越门位置不能重叠，即不能满足 \(N_1 = N_2\) 和 \(M_1 = M_2\) ；两个穿越门位置也不能位于左上角 \((1 , 1)\) 和右下角 \((N, M)\) ；第一个穿越门位置要在第二个穿越门前边或者上边。

【输出格式】

输出一个整数，表示黑精灵去白精灵家最短路线需要走多少步（可借助穿越门，减少步数），如果没有能到达白精灵家的路线或者其它情况统一输出数字 0 。

样例 1

【样例 1 输入】

3 4
2 3
3 1

【样例 1 输出】

4

【样例 1 解释】

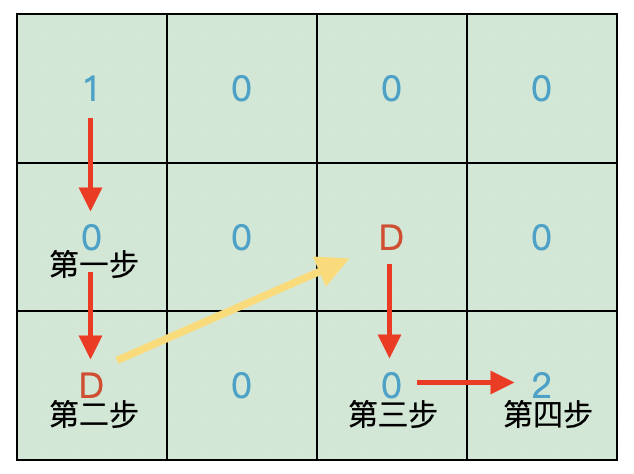
给出一个 \(3 \times 4\) 矩阵方格。并给出第一个穿越门的坐标位置 \(N_1 , M_1 (2 , 3)\) ，第二个穿越门的坐标位置 \(N_2 , M_2 (3 , 1)\) ，已知黑精灵初始坐标位置左上角 \((1 , 1)\) ，白精灵坐标位置右下角 \((N , M)\) 。

假设用两个大写字母 D 表示矩阵方格中穿越门位置，1 代表黑精灵，2 代表白精灵，用数字 0 表示剩余矩阵方格。

如下图所示：

按照穿行矩阵方格要求为左上角方格的黑精灵到右下角方格白精灵家找一条最短路线，计算出最短路线的步数。

路线：从黑精灵初始位置 \((1 , 1)\) 到正下方方格 \((2 , 1)\) 走 \(1\) 步，正下方方格 \((2 , 1)\) 到其下方穿越门 \((3 , 1)\) 走 \(1\) 步，然后穿越到另一扇穿越门 \((2 , 3)\) 向正下方 \((3 , 3)\) 走 \(1\) 步，最后到达白精灵家 \((3 , 4)\) 需要走 \(1\) 步，故最短路线需要 \(4\) 步。