背景

king大佬思考了一个问题：7的10次方，怎样算比较快？

方法1：最朴素的想法，7*7=49，49*7=343，... 一步一步算，共进行了9次乘法。

这样算无疑太慢了，这时他想到， 也许可以拆分问题.

方法2：先算7*7得49，则7的5次方为49*49*7，再算它的平方，共进行了4次乘法。

模仿这样的过程，我们得到了快速幂算法。

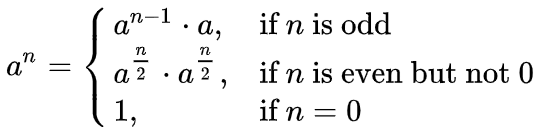
同时有(a * a)%p == (a%p) * (a%p),请注意 每一步都取模 以免超过所能存储的最大数据范围

题目描述

给你三个整数 a,b,p
求 a^b mod p（a的b次方%p）
时间限制： 200ms
Tips：可以认为评测机1s内可以进行100,000,000次计算
int类型的变量可最大储存2∧31-1，long long则是2∧63-1

输入格式

输入只有一行三个整数，分别代表 a,b,p，中间以空格隔开。
保证0<a,b,p<= 2^33
请小心溢出

输出格式

输出一行一个字符串

a^b mod p=s
其中 a,b,p 分别为题目给定的值， s 为运算结果。
注意 空格

样例

输入

3 4 10

输出

3^4 mod 10=1