题目背景

B君和G君在过街天桥上。

B君：「又到冬天啦，算起来到大学已经三年多了」

G君：「是呀」

B君：「街上的情侣又多起来了，想想三年之前，我也是这样……」

G君：「？？」

B君：「……在天桥上看情侣的！」

G君：「唔。」

B君：「不过这次有你陪我了呢~」

G君：「……」

B君：「诶诶，我有个问题想问你~」

G君：「问吧」

B君：「假设 \(n=3^m\) 个人一起玩cei ding ke」

G君：「啊咧？cei ding ke 是什么？」

B君：「就是石头剪刀布~，我们也叫钉钢锤」

G君：「你就问这个？」

B君：「你等会，我还没说完呢」

任务描述

\(n = 3^m\) 个人在玩石头剪刀布， 一共有 \(t\) 轮游戏，每轮有 \(m\) 次石头剪刀布。

在同一轮的 \(m\) 次游戏中，每个人的决策必须是提前确定的，也就是说不能采用随机策略，也不能根据前若干局的结果决定下一局的决策； 这样，显然一共有 \(n = 3^m\) 种决策。

这 \(n = 3^m\) 个人会采取两两不同的决策。
为了方便表达，对于第 \(x\)（\(0 \leq x < n\)）个人，将 \(x\) 转换成三进制得到一个\(m\)位的数。
其中 \(0\) 表示剪刀，\(1\) 表示石头，\(2\) 表示布。就得到了第 \(x\) 个人采取的策略。

由于编号是固定的，因此每个人在不同轮的 \(m\) 次游戏中都会采取同一套决策。

第 \(x\) 个人在最初时有一个分数 \(f_{0, x}\)。

在第 \(i\) 轮中，他将和另一个人 \(y\) 进行 \(m\) 次的石头剪刀布的比赛。

我们用 \(W \left( x, y \right)\) 表示 \(x\) 在和 \(y\) 的 \(m\) 次比赛中赢的次数；
用 \(L \left( x, y \right)\) 表示 \(x\) 在和 \(y\) 的 \(m\) 次比赛中输的次数。

在第 \(i\) 轮结束之后，第 \(x\) 个人分数是：

\[ f_{i, x} = \sum_{0 \leq y < n} f_{i-1, y} b_{u, v} \]

其中 \(u = W \left( x, y \right) = L \left( y, x \right), v = L \left( x, y \right) = W \left( y, x \right)\)，平局不计入次数；
\(b_{u,v}\) 则是一个给定的评分数组。

注意即使 \(y\) 和 \(x\) 一样（自己转移到自己）也会乘上一个系数 \(b_{0, 0}\)（即自己跟自己打全为平局）。

显然随着轮数越来越多，分数也会越来越大， 这个计分系统和我们平时用的计算机一样，也会溢出。
当要储存的分数 \(f\) 大于等于 \(p\) 的时候，就会变成 \(f \bmod p\)。

B君想知道 \(t\) 轮之后所有人的分数，也就是 \(f_{t, 0}, f_{t, 1}, \ldots, f_{t, n - 1}\)。

G君：「诶，我发现这个数 \(p\) 有特殊的性质诶！不存在两个正整数，使得他们倒数的和等于 \(3/p\)！」

B君：「G君好棒！不过这个题怎么做呢？」

输入

第一行三个整数，表示 \(m, t, p\)。

第二行有 \(n = 3^m\) 个整数，表示 \(f_{0, 0}, f_{0, 1}, \ldots, f_{0, n - 1}\)。保证 \(0 \leq f_{0, i} < p\)。

接下来的部分是一个数组 \(b\)，第 \(1\) 行 \(m + 1\) 个数，第 \(2\) 行 \(m\) 个数……第 \(m + 1\) 行 \(1\) 个数。

其中第 \(i\) 行的第 \(j\) 个数为 \(b_{i-1, j-1}\)（\(i, j \ge 1, i + j - 2 \le m\)），保证 \(0 \leq b_{i, j} < p\)。

不存在两个正整数，使得他们倒数的和等于 \(3/p\)。 即不存在正整数 \(x, y > 0\)，使得 \(1/x + 1/y = 3/p\)。

输出

输出 \(n = 3^m\) 行，每行一个整数，表示每个人最终的得分。

其中第 \(i\) 行表示第 \(i\) 个人的得分 \(f_{t, i}\)。

样例一

输入

1  1  10009
10  100  1000
2  3
4

输出

4320
3240
2430

样例二

输入

2 3 103
7 8 9 10 11 12 13 14 15
1 2 3
4 5
6

输出

96
8
73
38
53
15
27
42
4

数据范围限制

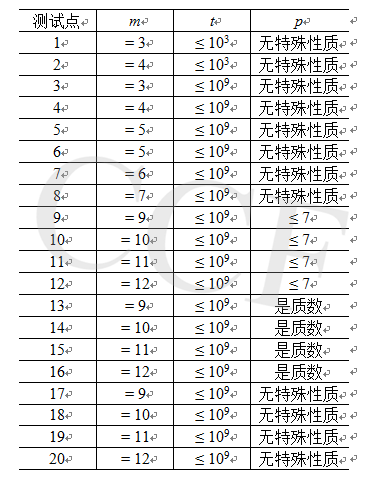
对于所有数据，\(0 \leq m \leq 12\)，\(0 \leq t \leq 10^{9}\)，\(1 \leq p \leq 10^{9}\)。

限制

每个测试点时限：2秒
内存限制：512MB

来源

清华集训2016