题目描述

\(\pi\text{+}e\) 在高中上数学课时经常睡觉，然而每次考试都能 \(AK\)，这让他的同桌叶子很是膜拜。

某天，老师在课上讲二项分布的题目：

(2010天津,18改)
某射手每次射击击中目标的概率 \(p=1/3\), 且各次射击的结果相互独立, 互不影响。
记4次中击中的次数为 \(X\), 求 \(X\) 的数学期望与期望的方差。
(答案：4/3，8/9)

老师说：“这个，二项分布的期望就是 \(np\)，方差就是 \(np(1-p)\)，不信你们自己课后回去算。”

\(\pi\text{+}e\) 一听有附加题，马上打起了精神，
三下五除二用了他的黑科技“母函数求导”就轻而易举的解决了这个问题。
顺便帮叶子也给科普了一下。

2016年暑假的某天，\(\pi\text{+}e\) 突然想起了这件事。
他想了想，把原来的问题加强了一下，变成下面这个样子：

有一个多项式函数 \(f(x)\)，最高次幂为 \(x^m\)，定义变换 \(Q\)：

\[Q(f,n,x) = \sum_{k = 0}^{n}f(k){n\choose k}x^k(1 - x) ^{n - k}\]

现在给定函数 \(f\) 和 \(n,x\)，求 \(Q(f,n,x)\bmod 998244353\)。

然而，众所周知，高考考完是会掉很多智商的。
\(\pi\text{+}e\) 发现自己已经忘记掉怎么用的黑科技了；
他打电话给叶子，叶子也说不记得了。

你能帮帮他吗？

出于某种原因，函数 \(f\) 由点值形式给出，即给定 \(a_0,a_1,\cdots,a_m\) 共 \(m+1\) 个数，\(f(x)=a_x\)。可以证明该函数唯一。

输入

第一行，三个整数 \(n,m,x\)，意义如前所述。

第二行，共 \(m+1\) 个整数，表示 \(a_0,a_1,\cdots,a_m\)。

输出

一个数表示答案，请对 \(998,244,353\) 取模。

样例一

输入

4 1 332748118
0 1

输出

332748119

解释

注意到 \(332748118 \equiv \frac{1}{3} \pmod{ 998244353 }\), \(332748119 \equiv \frac{4}{3} \pmod{ 998244353 }\), \(f(x)=x\), 题目中所求的表达式为：

\[\sum_{k=0}^4 k{4\choose k}\left(\frac{1}{3}\right)^k\left(\frac{2}{3}\right)^{4-k}=\frac{4}{3}\]

此即为题目开头二项分布例题计算期望的表达式。

样例二

输入

4 3 12
0 1 8 27

输出

46704

解释

经计算可得 \(f(x)=x^3\)

样例三

见样例数据下载。

限制与约定

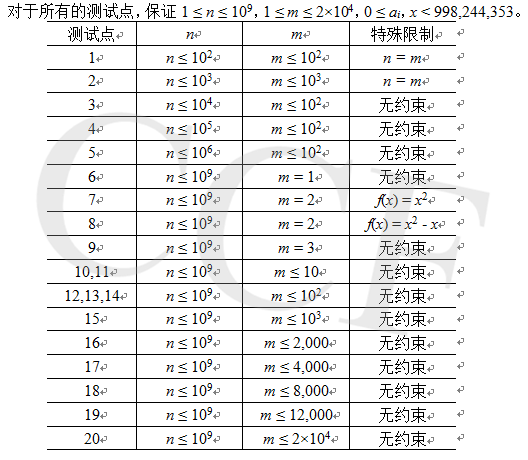
对于所有的测试点，保证 \(1 \le n \le 10^{9},\ 1 \le m \le 2 \times 10^{4},\ 0\le a_i,x< 998,244,353\)。

数据范围限制

来源

清华集训2016